
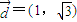 的直线与抛物线C相交于A,B两点,求使∠AFB为钝角时实数m的取值范围;
的直线与抛物线C相交于A,B两点,求使∠AFB为钝角时实数m的取值范围;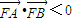 ,从而可得不等式,由此可求实数m的取值范围;
,从而可得不等式,由此可求实数m的取值范围;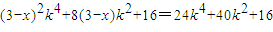 对任意k恒成立,此时直线不存在;②对参数m讨论,可得结论.
对任意k恒成立,此时直线不存在;②对参数m讨论,可得结论.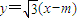 代入y2=8x得3x2-(6m+8)x+3m2=0,
代入y2=8x得3x2-(6m+8)x+3m2=0,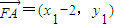 ,
,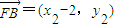 ,
,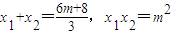 .….(6分)
.….(6分)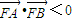 ,∴(x1-2)(x2-2)+y1y2<0,
,∴(x1-2)(x2-2)+y1y2<0,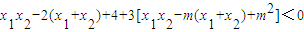 ,
,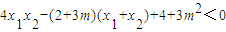 ,….(8分)
,….(8分)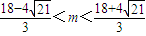 ,
,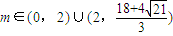 .….(10分)
.….(10分)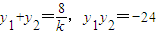 ,
,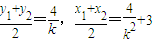 ,∴AB中点
,∴AB中点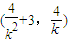 ,….(12分)
,….(12分)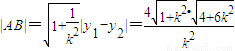 .….(13分)
.….(13分)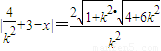 ,….(14分)
,….(14分)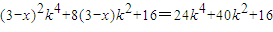 对任意k恒成立,
对任意k恒成立,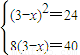 无解,∴这样的直线不存在. ….(16分)
无解,∴这样的直线不存在. ….(16分)

科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| d |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OE |
| OA |
| OB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com