
°Њћвƒњ°њЋж„≈„ ±Њ –≥°µƒ«њ ∆љш»л£ђї•Ѕ™Ќшє≤ѕнµ•≥µ°∞Їц»з“ї“єіЇЈзјі°±£ђ±й≤ЉЅЋ“їґюѕя≥« –µƒіуљ÷–°ѕп.ќ™ЅЋљвє≤ѕнµ•≥µ‘Џ![]() –µƒ є”√«йњц£ђƒ≥µч≤йїъєєљи÷ъЌш¬зљш––ЅЋќ Њнµч≤й£ђ≤Ґі”≤ќ”лµч≤йµƒЌш”—÷–Ћжїъ≥й»°ЅЋ200»Ћљш––≥й—щЈ÷ќц£ђµ√µљѕ¬±н£®µ•ќї£Ї»Ћ£©£Ї
–µƒ є”√«йњц£ђƒ≥µч≤йїъєєљи÷ъЌш¬зљш––ЅЋќ Њнµч≤й£ђ≤Ґі”≤ќ”лµч≤йµƒЌш”—÷–Ћжїъ≥й»°ЅЋ200»Ћљш––≥й—щЈ÷ќц£ђµ√µљѕ¬±н£®µ•ќї£Ї»Ћ£©£Ї
Њ≠≥£ є”√ | ≈Љґыїт≤ї”√ | ЇѕЉ∆ | |
30ЋкЉ∞“‘ѕ¬ | 70 | 30 | 100 |
30Ћк“‘…ѕ | 60 | 40 | 100 |
ЇѕЉ∆ | 130 | 70 | 200 |
£®1£©ЄщЊЁ“‘…ѕ эЊЁ£ђƒ№Јс‘ЏЈЄінќуµƒЄ≈¬ ≤ї≥ђєэ0.15µƒ«∞ћбѕ¬»ѕќ™![]() – є”√є≤ѕнµ•≥µ«йњц”лƒкЅд”–єЎ£њ
– є”√є≤ѕнµ•≥µ«йњц”лƒкЅд”–єЎ£њ
£®2£©ѕ÷і”Ћщ”–≥й»°µƒ30Ћк“‘…ѕµƒЌш√с÷–јы”√Ј÷≤г≥й—щ≥й»°5»Ћ£ђ
![]() «у’в5»Ћ÷–Њ≠≥£ є”√°Ґ≈Љґыїт≤ї”√є≤ѕнµ•≥µµƒ»Ћ э£ї
«у’в5»Ћ÷–Њ≠≥£ є”√°Ґ≈Љґыїт≤ї”√є≤ѕнµ•≥µµƒ»Ћ э£ї
![]() і”’в5»Ћ÷–£ђ‘ЏЋжїъ—°≥ц2»Ћ‘щЋЌ“їЉюјс∆Ј£ђ«у—°≥цµƒ2»Ћ÷–÷Ѕ…ў”–1»ЋЊ≠≥£ є”√є≤ѕнµ•≥µµƒЄ≈¬ .
і”’в5»Ћ÷–£ђ‘ЏЋжїъ—°≥ц2»Ћ‘щЋЌ“їЉюјс∆Ј£ђ«у—°≥цµƒ2»Ћ÷–÷Ѕ…ў”–1»ЋЊ≠≥£ є”√є≤ѕнµ•≥µµƒЄ≈¬ .
≤ќњЉєЂ љ£Ї 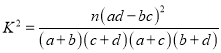 £ђ∆д÷–
£ђ∆д÷–![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
°Њір∞Є°њ(1)Љыљвќц£®2£©ҐўЉыљвќцҐЏ![]() .
.
°Њљвќц°њ ‘ћвЈ÷ќц£Ї£®1£©Љ∆Ћгk2£ђ”л2.027±»љѕіу–°µ√≥цљб¬џ£ђ
£®2£©£®i£©ЄщЊЁЈ÷≤г≥й—щЉіњ…«у≥ц£ђ
£®ii£©…и’в5»Ћ÷–£ђЊ≠≥£ є”√є≤ѕнµ•≥µµƒ3»ЋЈ÷±рќ™a£ђb£ђc£ї≈Љґыїт≤ї”√є≤ѕнµ•≥µµƒ2»ЋЈ÷±рќ™d£ђe£ђЄщЊЁє≈µдЄ≈¬ єЂ љЉ∆ЋгЉіњ…£Ѓ
‘ћвљвќц£Ї
£®1£©”…Ѕ–Ѕ™±нњ…÷™£ђ ![]() .
.
“тќ™![]() £ђ
£ђ
Ћщ“‘ƒ№‘ЏЈЄінќуµƒЄ≈¬ ≤ї≥ђєэ0.15µƒ«∞ћбѕ¬»ѕќ™![]() – є”√є≤ѕнµ•≥µ«йњц”лƒкЅд”–єЎ.
– є”√є≤ѕнµ•≥µ«йњц”лƒкЅд”–єЎ.
£®2£©£®i£©“јћв“вњ…÷™£ђЋщ≥й»°µƒ5√ы30Ћк“‘…ѕµƒЌш”—÷–£ђЊ≠≥£ є”√є≤ѕнµ•≥µµƒ”–![]() £®»Ћ£©£ђ≈Љґыїт≤ї”√є≤ѕнµ•≥µµƒ”–
£®»Ћ£©£ђ≈Љґыїт≤ї”√є≤ѕнµ•≥µµƒ”–![]() £®»Ћ£©.
£®»Ћ£©.
£®ii£©…и’в5»Ћ÷–£ђЊ≠≥£ є”√є≤ѕнµ•≥µµƒ3»ЋЈ÷±рќ™![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ї≈Љґыїт≤ї”√є≤ѕнµ•≥µµƒ2»ЋЈ÷±рќ™
£ї≈Љґыїт≤ї”√є≤ѕнµ•≥µµƒ2»ЋЈ÷±рќ™![]() £ђ
£ђ ![]() .‘ті”5»Ћ÷–—°≥ц2»ЋµƒЋщ”–њ…ƒ№љбєыќ™
.‘ті”5»Ћ÷–—°≥ц2»ЋµƒЋщ”–њ…ƒ№љбєыќ™![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() £ђ
£ђ ![]() є≤10÷÷.
є≤10÷÷.
∆д÷–√ї”–1»ЋЊ≠≥£ є”√є≤ѕнµ•≥µµƒњ…ƒ№љбєыќ™![]() є≤1÷÷£ђ
є≤1÷÷£ђ
є —°≥цµƒ2»Ћ÷–÷Ѕ…ў”–1»ЋЊ≠≥£ є”√є≤ѕнµ•≥µµƒЄ≈¬ ![]() .
.


 ‘ƒґЅњм≥µѕµЅ–ір∞Є
‘ƒґЅњм≥µѕµЅ–ір∞Є
| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»фєЎ”Џ![]() µƒ≤їµ» љ
µƒ≤їµ» љ![]() «°Ї√”–4Єц’ы эљв£ђ‘т µ э
«°Ї√”–4Єц’ы эљв£ђ‘т µ э![]() µƒ»°÷µЈґќІ «£® £©
µƒ»°÷µЈґќІ «£® £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™»ЂЉѓU={1£ђ2£ђ3£ђ4£ђ5£ђ6£ђ7}£ђЉѓЇѕA={1£ђ3£ђ7}£ђB={x|x=log2£®a+1£©£ђa° A}£ђ‘тA°…B=£® £©
A.{1£ђ3}
B.{5£ђ6}
C.{4£ђ5£ђ6}
D.{4£ђ5£ђ6£ђ7}
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ£®1£©“—÷™![]() «∆жЇѓ э£ђ«у≥£ эmµƒ÷µ£ї
«∆жЇѓ э£ђ«у≥£ эmµƒ÷µ£ї
£®2£©ї≠≥цЇѓ э![]() µƒЌЉѕу£ђ≤Ґјы”√ЌЉѕуїЎір£Їkќ™Їќ÷µ ±£ђЈљ≥ћ
µƒЌЉѕу£ђ≤Ґјы”√ЌЉѕуїЎір£Їkќ™Їќ÷µ ±£ђЈљ≥ћ![]() ќёљв£њ”–“їљв£њ”–Ѕљљв£њ
ќёљв£њ”–“їљв£њ”–Ѕљљв£њ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“‘∆љ√ж÷±љ«„ш±кѕµµƒ‘≠µгќ™ЉЂµг£ђ ![]() ÷б’э∞л÷бќ™ЉЂ÷бљ®ЅҐЉЂ„ш±кѕµ£ђ“—÷™‘≤
÷б’э∞л÷бќ™ЉЂ÷бљ®ЅҐЉЂ„ш±кѕµ£ђ“—÷™‘≤![]() µƒЉЂ„ш±кЈљ≥ћќ™
µƒЉЂ„ш±кЈљ≥ћќ™![]() £ђ÷±ѕя
£ђ÷±ѕя![]() µƒ≤ќ эЈљ≥ћќ™
µƒ≤ќ эЈљ≥ћќ™![]() £®
£®![]() ќ™≤ќ э£©£ђ»ф
ќ™≤ќ э£©£ђ»ф![]() ”л
”л![]() љї”Џ
љї”Џ![]() Ѕљµг.
Ѕљµг.
£®Ґс£©«у‘≤![]() µƒ÷±љ«„ш±кЈљ≥ћ£ї
µƒ÷±љ«„ш±кЈљ≥ћ£ї
£®Ґт£©…и![]() £ђ«у
£ђ«у![]() µƒ÷µ.
µƒ÷µ.
°Њір∞Є°њ£®1£©![]() £ї£®2£©1.
£ї£®2£©1.
°Њљвќц°њ ‘ћвЈ÷ќц£Ї£®1£©ѕ»ЄщЊЁ![]() љЂ‘≤
љЂ‘≤![]() µƒЉЂ„ш±кЈљ≥ћїѓќ™÷±љ«„ш±кЈљ≥ћ£ї£®2£©ѕ»љЂ÷±ѕя≤ќ эЈљ≥ћµч’ыїѓЉт
µƒЉЂ„ш±кЈљ≥ћїѓќ™÷±љ«„ш±кЈљ≥ћ£ї£®2£©ѕ»љЂ÷±ѕя≤ќ эЈљ≥ћµч’ыїѓЉт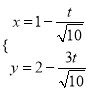 £ђ‘ўљЂ÷±ѕя≤ќ эЈљ≥ћіъ»л‘≤÷±љ«„ш±кЈљ≥ћ£ђЄщЊЁ≤ќ эЉЄЇќ“в“еµ√
£ђ‘ўљЂ÷±ѕя≤ќ эЈљ≥ћіъ»л‘≤÷±љ«„ш±кЈљ≥ћ£ђЄщЊЁ≤ќ эЉЄЇќ“в“еµ√![]() £ђ„оЇујы”√ќ§іпґ®јн«уљв
£ђ„оЇујы”√ќ§іпґ®јн«уљв
‘ћвљвќц£Ї£®Ґс£©”…![]() £ђµ√
£ђµ√![]() £ђ
£ђ
![]()
£®Ґт£©∞—![]() £ђ
£ђ ![]()
іъ»л…ѕ љµ√![]() £ђ
£ђ
°а![]() £ђ‘т
£ђ‘т![]() £ђ
£ђ ![]() £ђ
£ђ
![]()
![]()
![]() .
.
°Њћв–Ќ°њљвірћв
°Њљб ш°њ
23
°Њћвƒњ°њ÷§√ч£Ї£®Ґс£©“—÷™![]() «’э µ э£ђ«“
«’э µ э£ђ«“![]() .«у÷§£Ї
.«у÷§£Ї ![]() £ї
£ї
£®Ґт£©“—÷™![]() £ђ«“
£ђ«“![]() £ђ
£ђ ![]() £ђ
£ђ ![]() .«у÷§£Ї
.«у÷§£Ї ![]() ÷–÷Ѕ…ў”–“їЄц «ЄЇ э.
÷–÷Ѕ…ў”–“їЄц «ЄЇ э.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™ эЅ–![]() «єЂ≤о≤їќ™0µƒµ»≤о эЅ–£ђ
«єЂ≤о≤їќ™0µƒµ»≤о эЅ–£ђ ![]() «“
«“![]() ≥…µ»±» эЅ–£Ѓ
≥…µ»±» эЅ–£Ѓ
(1)«у эЅ–{an}µƒЌ®ѕоєЂ љ£ї
(2)…и![]() £ђ«у эЅ–
£ђ«у эЅ–![]() µƒ«∞nѕоЇЌ
µƒ«∞nѕоЇЌ![]() .
.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™Ќ÷‘≤ ![]() µƒјл–ƒ¬
µƒјл–ƒ¬ ![]() £ђєэµгA£®0£ђ©Бb£©ЇЌB£®a£ђ0£©µƒ÷±ѕя”л‘≠µгµƒЊајлќ™
£ђєэµгA£®0£ђ©Бb£©ЇЌB£®a£ђ0£©µƒ÷±ѕя”л‘≠µгµƒЊајлќ™ ![]() £Ѓ
£Ѓ
£®1£©«уЌ÷‘≤µƒЈљ≥ћ£ї
£®2£©“—÷™ґ®µгE£®©Б1£ђ0£©£ђ»ф÷±ѕяy=kx+2£®k°ў0£©”лЌ÷‘≤љї”ЏC°ҐDЅљµг£ђќ £Ї «Јсіж‘Џkµƒ÷µ£ђ є“‘CDќ™÷±Њґµƒ‘≤єэEµг£њ«лЋµ√чјн”…£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“‘ѕ¬єЎ”Џ‘≤„ґ«ъѕяµƒ√ьћв÷–
Ґў…и![]() «ЅљЄцґ®µг£ђ
«ЅљЄцґ®µг£ђ ![]() ќ™Ј«Ѕг≥£ э£ђ»ф
ќ™Ј«Ѕг≥£ э£ђ»ф![]() £ђ‘тґѓµг
£ђ‘тґѓµг![]() µƒємЉ£ќ™ЋЂ«ъѕяµƒ“ї÷І£їҐЏєэґ®‘≤
µƒємЉ£ќ™ЋЂ«ъѕяµƒ“ї÷І£їҐЏєэґ®‘≤![]() …ѕ“їґ®µг
…ѕ“їґ®µг![]() „ч‘≤µƒґѓѕ“
„ч‘≤µƒґѓѕ“![]() £ђ
£ђ ![]() ќ™„ш±к‘≠µг£ђ»ф
ќ™„ш±к‘≠µг£ђ»ф![]() £ђ‘тґѓµг
£ђ‘тґѓµг![]() µƒємЉ£ќ™Ќ÷‘≤£їҐџЈљ≥ћ
µƒємЉ£ќ™Ќ÷‘≤£їҐџЈљ≥ћ![]() µƒЅљЄщњ…Ј÷±р„чќ™Ќ÷‘≤ЇЌЋЂ«ъѕяµƒјл–ƒ¬ £їҐ№ЋЂ«ъѕя
µƒЅљЄщњ…Ј÷±р„чќ™Ќ÷‘≤ЇЌЋЂ«ъѕяµƒјл–ƒ¬ £їҐ№ЋЂ«ъѕя![]() ”лЌ÷‘≤
”лЌ÷‘≤![]() ”–ѕаЌђµƒљєµг.
”–ѕаЌђµƒљєµг.
∆д÷–’ж√ьћвµƒ–тЇ≈ «_______.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ”–“ї÷÷іу–Ќ…ћ∆Ј£ђA£ђBЅљµЎґЉ”–≥ц џ£ђ«“ЉџЄсѕаЌђ£ђƒ≥µЎЊ”√сі”ЅљµЎ÷Ѓ“їєЇµ√…ћ∆ЈЇу£ђ‘ЋїЎµƒЈ—”√ «£Ї√њµ•ќїЊајлAµЎµƒ‘ЋЈ— «BµЎ‘ЋЈ—µƒ3±ґ£Ѓ“—÷™A£ђBЅљµЎѕаЊа10 km£ђєЋњЌ—°AїтBµЎєЇ¬т’вЉю…ћ∆Јµƒ±к„Љ «£Ї∞ьј®‘ЋЈ—ЇЌЉџЄсµƒ„№Ј—”√љѕµЌ£Ѓ«уA£ђBЅљµЎµƒ џїх«ш”тµƒЈ÷љзѕяµƒ«ъѕя–ќ„і£ђ≤Ґ÷Є≥ц«ъѕя…ѕ°Ґ«ъѕяƒЏ°Ґ«ъѕяЌвµƒЊ”√с”¶»зЇќ—°‘сєЇїхµЎµг£Ѓ

≤йњіір∞ЄЇЌљвќц>>
∞ўґ»÷¬–≈ - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com