
| π |
| 6 |
| 2π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 2 |
| 2 |
| B |
| 1 |
| B |
| 2 |
| B |
| -2 |
| B |
| 2 |
| B |
| 2 |
| B |
|
| π |
| 2 |
| π |
| 2 |
| 3 |
| ||
| 3 |
| 2 |
| B |
| 3 |
| 2 |
| B |
| ||
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| B |
| π |
| 4 |
| 2 |
| B |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |


科目:高中数学 来源:2006年高考第一轮复习数学:7.1 直线的方程(解析版) 题型:解答题
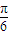 <α<
<α<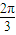 ,试求B的取值范围;
,试求B的取值范围;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| π |
| 6 |
| 2π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)试将α表示为B的函数;
(2)若![]() <α<
<α<![]() ,试求B的取值范围;
,试求B的取值范围;
(3)若B∈(-∞,-2)∪(1,+∞),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)试将α表示为B的函数;
(2)若![]() <α<
<α<![]() ,试求B的取值范围;
,试求B的取值范围;
(3)若B∈(-∞,-2)∪(1,+∞),求α的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com