
分析 (Ⅰ)通过Sn=$\frac{3}{2}$n2+$\frac{n}{2}$,当n≥2时利用an=Sn-Sn-1可知an=3n-1,且当n=1时也成立,从而an=3n-1;通过b1=2、bn=2bn-1可知${b}_{n}={2}^{n}$;
(Ⅱ)通过an=3n-1、${b}_{n}={2}^{n}$可知cn=3•2n-1,进而Sn=3•2n+1-n-6,从而问题转为求不等式3•2n+1-n-6>6•2n+n2-8n的整数解,计算即可.
解答 解:(Ⅰ)∵Sn=$\frac{3}{2}$n2+$\frac{n}{2}$,
∴当n=1时,a1=S1=$\frac{3}{2}$+$\frac{1}{2}$=2,
当n≥2时,Sn-1=$\frac{3}{2}$(n-1)2+$\frac{n-1}{2}$,
∴an=Sn-Sn-1
=($\frac{3}{2}$n2+$\frac{n}{2}$)-[$\frac{3}{2}$(n-1)2+$\frac{n-1}{2}$]
=3n-1,
又∵a1=2满足an=3n-1,
∴数列{an}的通项an=3n-1;
∵b1=2、bn=2bn-1,
∴数列{bn}的通项${b}_{n}={2}^{n}$;
(Ⅱ)∵an=3n-1,${b}_{n}={2}^{n}$,
∴cn=${a}_{{b}_{n}}$=3•2n-1,
∴Sn=3•$\frac{2(1-{2}^{n})}{1-2}$-n=3•2n+1-n-6,
∵Sn>6•2n+n2-8n,
即3•2n+1-n-6>6•2n+n2-8n,
化简得:n2-7n+6<0,
解得1<n<6,(n∈N*)
∴A={2,3,4,5}.
点评 本题考查数列的通项和前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
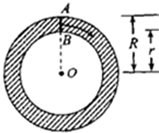 如图,我们知道圆环是线段AB绕圆心O旋转一周所形成的平面图形,所以,圆环的面积S=π(R2-r2)=(R-r)×2π×$\frac{R+r}{2}$可以看作是以线段AB=R-r为宽,以AB的中心绕圆心O旋转一周所形成的圆的周长2π×$\frac{R+r}{2}$为长的矩形面积.请将上述想法拓展到空间,并解决下列问题:若将平面区域M={(x,y)|(x-2)2+y2≤1}绕y轴旋转一周,则所形成的旋转体的体积是4π2.
如图,我们知道圆环是线段AB绕圆心O旋转一周所形成的平面图形,所以,圆环的面积S=π(R2-r2)=(R-r)×2π×$\frac{R+r}{2}$可以看作是以线段AB=R-r为宽,以AB的中心绕圆心O旋转一周所形成的圆的周长2π×$\frac{R+r}{2}$为长的矩形面积.请将上述想法拓展到空间,并解决下列问题:若将平面区域M={(x,y)|(x-2)2+y2≤1}绕y轴旋转一周,则所形成的旋转体的体积是4π2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-$\frac{π}{4}$ | B. | x=$\frac{π}{4}$ | C. | x=$\frac{π}{8}$ | D. | x=-$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 把正整数按“S”型排成了如图所示的三角形数表,第n行有n个数,对于第n行按从左往右的顺序依次标记第1列,第2列,…,第m列,(比如三角形数表中12在第5行第4列,18在第6行第3列),则三角形数表中2015在( )
把正整数按“S”型排成了如图所示的三角形数表,第n行有n个数,对于第n行按从左往右的顺序依次标记第1列,第2列,…,第m列,(比如三角形数表中12在第5行第4列,18在第6行第3列),则三角形数表中2015在( )| A. | 第63行第2列 | B. | 第62行第12列 | C. | 第64行第30列 | D. | 第64行第60列 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com