解:(Ⅰ)
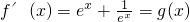
,
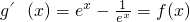
,
∴直线l
1的斜率
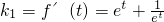
,直线l
2的斜率

,
令k
1=k
2,得
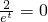
,此方程没有实数解,∴不论t取何实数值,直线l
1与l
2恒相交.
(Ⅱ)直线l
1的方程为:y=f(t)+g(t)(x-t),…①
直线l
2的方程为:y=g(t)+f(t)(x-t),…②
由①、②得:(g(t)-f(t))(x-t-1)=0.
∵

,∴x-t=1,又∵直线AB方程为x=t,直线AB垂直x轴,∴点P到直线AB的距离为1.
(Ⅲ)由(Ⅱ)可求得P(t+1,2e
t),
①∵
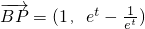
,
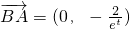
,
∴
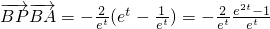
,
∵t<0,e
2t<1,∴

,
又∵
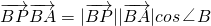
,
∴cos∠B>0,∠B恒为锐角.
②∵
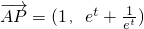
,
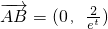
,
∴
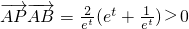
,
∴不论t取何值,∠A恒为锐角.
③∵
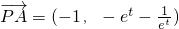
,
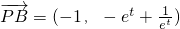
,∴
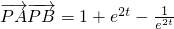
.
令
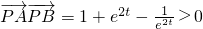
,得(e
2t)
2+e
2t-1>0,
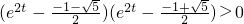
,
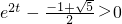
,
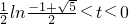
.
又∵
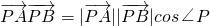
,∴cos∠P>0,∠P为锐角.
令
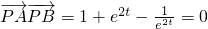
,得
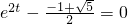
,
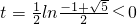
,
此时,cos∠P=0,∠P为直角;
令
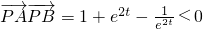
,得(e
2t)
2+e
2t-1<0,
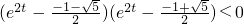
,
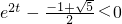
,
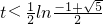
,此时,cos∠P<0,∠P为钝角.
综合①②③得:当
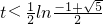
时,△PAB为钝角三角形;
当
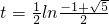
时,△PAB为直角三角形;
当
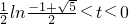
时,△PAB为锐角三角形.
分析:(Ⅰ)求出两个函数的导数,即得切线的斜率,令这两条切线的斜率相等,此方程无解,故这两条切线的斜率一定不相等,得到直线l
1与l
2恒相交.
(Ⅱ)用点斜式求得直线l
1和直线l
2的方程,求得交点P的横坐标满足x-t=1,又直线AB方程为x=t,直线AB垂直x轴,
故点P到直线AB的距离为 1.
(Ⅲ)利用两个向量的数量积的定义、数量积公式可得∠B恒为锐角,且∠A恒为锐角,令

分别小于0、等于
0、小于0,求出对应的t值,即得所求.
点评:本题考查导数的几何意义,点到直线的距离公式,两个向量的数量积的定义,数量积公式,三角形形状的判定,体现了分类讨论的数学思想.

 ,
, ,动直线x=t分别与函数y=f(x)、y=g(x)的图象分别交于点A(t,f(t))、B(t,g(t)),在点A处作函数y=f(x)的图象的切线,记为直线l1,在点B处作函数y=g(x)的图象的切线,记为直线l2.
,动直线x=t分别与函数y=f(x)、y=g(x)的图象分别交于点A(t,f(t))、B(t,g(t)),在点A处作函数y=f(x)的图象的切线,记为直线l1,在点B处作函数y=g(x)的图象的切线,记为直线l2.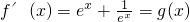 ,
,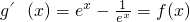 ,
,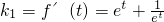 ,直线l2的斜率
,直线l2的斜率 ,
,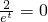 ,此方程没有实数解,∴不论t取何实数值,直线l1与l2恒相交.
,此方程没有实数解,∴不论t取何实数值,直线l1与l2恒相交. ,∴x-t=1,又∵直线AB方程为x=t,直线AB垂直x轴,∴点P到直线AB的距离为1.
,∴x-t=1,又∵直线AB方程为x=t,直线AB垂直x轴,∴点P到直线AB的距离为1.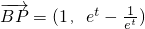 ,
,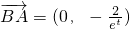 ,
,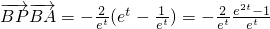 ,
, ,
,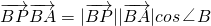 ,
,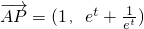 ,
,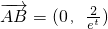 ,
,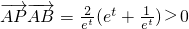 ,
,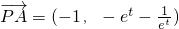 ,
,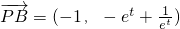 ,∴
,∴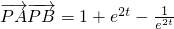 .
.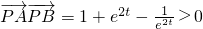 ,得(e2t)2+e2t-1>0,
,得(e2t)2+e2t-1>0,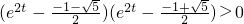 ,
,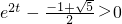 ,
,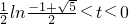 .
.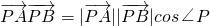 ,∴cos∠P>0,∠P为锐角.
,∴cos∠P>0,∠P为锐角.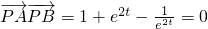 ,得
,得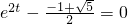 ,
,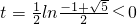 ,
,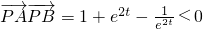 ,得(e2t)2+e2t-1<0,
,得(e2t)2+e2t-1<0,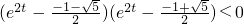 ,
,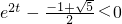 ,
,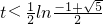 ,此时,cos∠P<0,∠P为钝角.
,此时,cos∠P<0,∠P为钝角.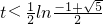 时,△PAB为钝角三角形;
时,△PAB为钝角三角形;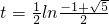 时,△PAB为直角三角形;
时,△PAB为直角三角形;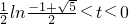 时,△PAB为锐角三角形.
时,△PAB为锐角三角形. 分别小于0、等于
分别小于0、等于
