
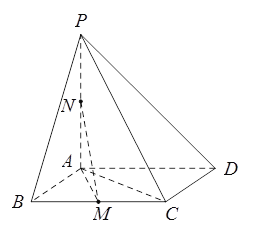
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() 平面
平面![]() ,点
,点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,且
的中点,且![]() ,
, ![]() .
.

(1)证明: ![]() 平面
平面![]() ;
;
(2)设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,当
,当![]() 在
在![]() 内变化时,求二面角
内变化时,求二面角![]() 的取值范围.
的取值范围.
【答案】(1) 见解析;(2) ![]() .
.
【解析】试题分析:(Ⅰ)根据直线与平面平行的判定定理,需在平面![]() 内找一条与
内找一条与![]() 平行的直线.结合题设可取取
平行的直线.结合题设可取取![]() 中点
中点![]() ,连接
,连接![]() , 易得四边形
, 易得四边形![]() 为平行四边形,从而得
为平行四边形,从而得![]() ,问题得证.
,问题得证.
(Ⅱ)思路一、首先作出二面角的平面角,即过棱BC上一点分别在两个平面内作棱BC的垂线.因为![]() ,点
,点![]() 分别为
分别为![]() 的中点,则
的中点,则![]() .连接
.连接![]() ,因为
,因为![]() 平面
平面![]() ,所以AM是PM在面ABC内的射影,所以
,所以AM是PM在面ABC内的射影,所以![]() ,所以
,所以![]() 即为二面角
即为二面角![]() 的平面角.再作出直线
的平面角.再作出直线![]() 与平面
与平面![]() 所成的角,即作出AC在平面PBC内的射影.由
所成的角,即作出AC在平面PBC内的射影.由![]() ,
, ![]() 且
且![]() 得
得![]() 平面
平面![]() ,从而平面
,从而平面![]() 平面
平面![]() .过点
.过点![]() 在平面
在平面![]() 内作
内作![]() 于
于![]() ,根据面面垂直的性质知
,根据面面垂直的性质知![]() 平面
平面![]() .连接
.连接![]() ,于是
,于是![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角.在
所成的角.在![]() 及
及![]() 中,找出
中,找出![]() 与
与![]() 的关系,即可根据
的关系,即可根据![]() 的范围求出
的范围求出![]() 的范围. 思路二、以
的范围. 思路二、以![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立空间直角坐标系,利用空间向量亦可求解.
轴,建立空间直角坐标系,利用空间向量亦可求解.
试题解析:(Ⅰ)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,
,
因为点![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]()
四边形![]() 为平行四边形,则
为平行四边形,则![]() 又
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
(Ⅱ)解法1:连接![]() ,因为
,因为![]() ,点
,点![]() 分别为
分别为![]() 的中点,则
的中点,则![]()
又![]() 平面
平面![]() ,则
,则![]() 所以
所以![]() 即为二面角
即为二面角![]() 的平面角
的平面角
又![]() ,所以
,所以![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]()
过点![]() 在平面
在平面![]() 内作
内作![]() 于
于![]() ,则
,则![]() 平面
平面![]() .
.
连接![]() ,于是
,于是![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角,即
所成的角,即![]() =
= ![]() .
.
在![]() 中,
中, ![]() ;
;
在![]() 中,
中, ![]() ,
, ![]() .
.
![]() ,
,
![]() ,
, ![]() .
.
又![]() ,
, ![]() .
.
即二面角![]() 取值范围为
取值范围为![]() .
.
解法2:连接![]() ,因为
,因为![]() ,点
,点![]() 分别为
分别为![]() 的中点,则
的中点,则![]()
又![]() 平面
平面![]() ,则
,则![]() 所以
所以![]() 即为二面角
即为二面角![]() 的平面角,设为
的平面角,设为![]()
以![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系,则
轴,建立如图所示的空间直角坐标系,则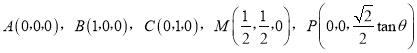 ,
,
于是, 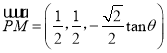 ,
, ![]() ,
, ![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则由![]() .
.
得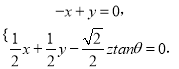
可取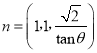 ,又
,又![]() ,
,
于是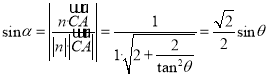 ,
,
![]() ,
,
![]() ,
, ![]() .
.
又![]() ,
, ![]() .
.
即二面角![]() 取值范围为
取值范围为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,过椭圆的上顶点
,过椭圆的上顶点![]() 和右顶点
和右顶点![]() 的直线与原点
的直线与原点![]() 的距离为
的距离为![]() ,
,
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在直线![]() 经过椭圆左焦点与椭圆
经过椭圆左焦点与椭圆![]() 交于
交于![]() ,
,![]() 两点,使得以线段
两点,使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() ?若存在,求出直线
?若存在,求出直线![]() 方程;若不存在,请说明理由.
方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50名学生组成一个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ……,第五组
……,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

(1)请估计学校1800名学生中,成绩属于第四组的人数;
(2)若成绩小于15秒认为良好,求该样本中在这次百米测试中成绩良好的人数;
(3)请根据频率分布直方图,求样本数据的众数、平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①第二象限角比第一象限角大;②设![]() 是第二象限角,则
是第二象限角,则![]() ;③三角形的内角是第一象限角或第二象限角;④函数
;③三角形的内角是第一象限角或第二象限角;④函数![]() 是最小正周期为
是最小正周期为![]() 的周期函数;⑤在△ABC中,若
的周期函数;⑤在△ABC中,若![]() ,则A>B.其中正确的是___________ (写出所有正确说法的序号)
,则A>B.其中正确的是___________ (写出所有正确说法的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线 ![]() 的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.
的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.
(1)若l的倾斜角为 ![]() ,
, ![]() 是等边三角形,求双曲线的渐近线方程;
是等边三角形,求双曲线的渐近线方程;
(2)设 ![]() ,若l的斜率存在,且|AB|=4,求l的斜率.
,若l的斜率存在,且|AB|=4,求l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用另一种形式表示下列集合:
(1){绝对值不大于3的整数};
(2){所有被3整除的数};
(3){x|x=|x|,x∈Z且x<5};
(4){x|(3x-5)(x+2)(x2+3)=0,x∈Z}.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(Ⅰ)当![]() 时,解不等式
时,解不等式![]() ;
;
(Ⅱ)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的和不大于
上的最大值与最小值的和不大于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,对称轴为坐标轴,一条渐近线方程为![]() ,右焦点
,右焦点![]() ,双曲线的实轴为
,双曲线的实轴为![]() ,
,![]() 为双曲线上一点(不同于
为双曲线上一点(不同于![]() ,
,![]() ),直线
),直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(![]() )求双曲线的方程.
)求双曲线的方程.
(![]() )证明
)证明![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t(天)(t∈N)的关系如图所示 
(1)写出销售价格P(元)和时间t(天)的函数解析式;
(2)若日销售量Q(件)与时间t(天)的函数关系是Q=﹣t+40(0≤t≤30,t∈N),求该商品的日销售金额y(元)与时间t(天)的函数解析式;
(3)问该产品投放市场第几天时,日销售金额最高?最高值为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com