Question

一扇形的周长为16，则当其半径r和圆心角α各为何值时，面积S最大，最大值为多少？

Answer 1

【答案】分析：设扇形的半径为r，弧长为l，利用周长关系，表示出扇形的面积，利用二次函数求出面积的最大值，以及圆心角的大小．
解答：解：设扇形的半径为r，弧长为l，则
l+2r=16，即l=16-2r（0＜r＜8）．
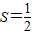
扇形的面积lr，将上式代入，
得S=（16-2r）r=-r²+8r
=-（r-4）²+16，
所以当且仅当r=4时，S有最大值16，
此时l=16-2×4=8，
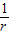
α==2 rad．
所以当α=2rad时，半径为4时，扇形的面积取最大值，最大值为16cm²．
点评：本题是基础题，考查扇形的周长，半径圆心角，面积之间的关系，考查计算能力．