
 如图所示的五面体ABCDFE中,四边形ABCD是矩形,AB∥EF,AD⊥平面ABEF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,P、Q分别为AE、BD的中点.
如图所示的五面体ABCDFE中,四边形ABCD是矩形,AB∥EF,AD⊥平面ABEF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,P、Q分别为AE、BD的中点.分析 (Ⅰ)连接AC,推导出PQ∥EC,由此能证明PQ∥平面BCE.
(Ⅱ)取EF的中点M,则AF⊥AM,以A为坐标原点,以AM,AF,AD所在直线分别为x,y,z轴建立空间直角坐标系,利用向量法能求出二面角A-DF-E的余弦值.
解答 证明:(Ⅰ)连接AC,∵四边形ABCD是矩形,且Q为BD的中点,
∴Q为AC的中点,
又在△AEC中,P为AE的中点,∴PQ∥EC,
∵EC?面BCE,PQ?面BCE,
∴PQ∥平面BCE…(5分)
解:(Ⅱ)如图,取EF的中点M,则AF⊥AM,
以A为坐标原点,以AM,AF,AD所在直线分别为x,y,z轴建立空间直角坐标系.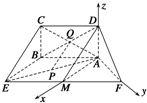 则A(0,0,0),D(0,0,1),M(2,0,0),F(0,2,0).
则A(0,0,0),D(0,0,1),M(2,0,0),F(0,2,0).
$\overrightarrow{AM}$=(2,0,0),$\overrightarrow{MF}$=(-2,2,0),$\overrightarrow{DF}$=(0,2,-1)…(7分)
设平面DEF的法向量为n=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{MF}=-2x+2y=0}\\{\overrightarrow{n}•\overrightarrow{DF}=2y-z=0}\end{array}\right.$,令x=1,则y=1,z=2,故$\overrightarrow{n}$=(1,1,2)是平面DEF的一个法向量…(9分)
∵AM⊥面ADF,∴$\overrightarrow{AM}$=(2,0,0)为平面ADF的一个法向量.
∴cos<n,$\overrightarrow{AM}$>=$\frac{n•\overrightarrow{AM}}{|n|•|\overrightarrow{AM}|}$=$\frac{2×1+0×1+0×2}{\sqrt{6}×2}$=$\frac{\sqrt{6}}{6}$.…(11分)
由图可知所求二面角为锐角,
∴二面角A-DF-E的余弦值为$\frac{\sqrt{6}}{6}$…(12分)
点评 本题考查线面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
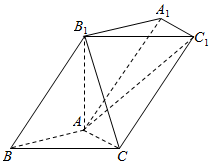 如图,在三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,BB1=2,∠ABB1=60°.
如图,在三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,BB1=2,∠ABB1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 二进制数11010(2)化为八进制数为42(8) | |
| B. | 若扇形圆心角为2弧度,且扇形弧所对的弦长为2,则这个扇形的面积为$\frac{1}{si{n}^{2}1}$ | |
| C. | 用秦九韶算法计算多项式f(x)=3x6+5x4+6x3-4x-5当x=3时的值时,v1=3v0+5=32 | |
| D. | 正切函数在定义域内为单调增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充分不必要条件 | D. | 必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“?x∈(1,+∞),使得x2+x-1<0”的否定是:“?x∈(1,+∞),均有x2+x-1≥0” | |
| C. | “x=-1是x2-5x-6=0”必要不充分条件 | |
| D. | 命题“已知x,y∈R,若x≠1,或y≠4则x+y≠5”为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com