
【题目】(1)求值:![]() . (2)求函数f(x)=
. (2)求函数f(x)=![]() 的定义域.
的定义域.
【答案】解:(1)![]()
=![]()
=![]() .
.
(2)函数f(x)=![]() 的定义域为:{x|
的定义域为:{x|![]() }
}
解得{x|x<0且x≠﹣1},
∴函数f(x)=![]() 的定义域为{x|x<0且x≠﹣1}.
的定义域为{x|x<0且x≠﹣1}.
【解析】(1)利用有理数指数幂的去处性质,把![]() 等价转化为
等价转化为![]() , 由此能求出结果.
, 由此能求出结果.
(2)函数f(x)=![]() 的定义域为:{x|
的定义域为:{x|![]() },由此能求出结果.
},由此能求出结果.
【考点精析】解答此题的关键在于理解函数的定义域及其求法的相关知识,掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零,以及对有理数指数幂的运算性质的理解,了解分数指数幂的运算性质:①
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零,以及对有理数指数幂的运算性质的理解,了解分数指数幂的运算性质:①![]() ;②
;②![]() ;③
;③![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(Ⅱ)当![]() 时,讨论函数
时,讨论函数![]() 单调性;
单调性;
(Ⅲ)是否存在实数![]() ,对任意的
,对任意的![]() ,
, ![]() ,且
,且![]() ,有
,有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)=x2﹣x+b,且f(log2a)=b,log2f(a)=2(a>0且a≠1),
(1)求a,b;
(2)求f(log2x)的最小值及相应 x的值;
(3)若f(log2x)>f(1)且log2f(x)<f(1),求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意x,[x]表示不超过x的最大整数,如[1.1]=1,[﹣2.1]=﹣3.定义R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0≤x≤1},则A中所有元素的和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为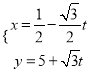 (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系.
轴的正半轴为极轴建立坐标系.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)射线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,能推断这个几何体可能是三棱台的是( ) 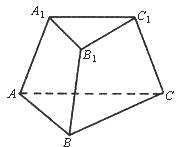
A.A1B1=2,AB=3,B1C1=3,BC=4
B.A1Bl=1,AB=2,BlCl=1.5,BC=3,A1C1=2,AC=3
C.AlBl=1,AB=2,B1Cl=1.5,BC=3,AlCl=2,AC=4
D.AB=A1B1 , BC=B1C1 , CA=C1A1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(4)与f(8)的值;
(2)解不等式f(x)﹣f(x﹣2)>3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com