
【题目】已知抛物线C:![]() =2px经过点
=2px经过点![]() (1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点,![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
【答案】(1) 取值范围是(-∞,-3)∪(-3,0)∪(0,1)
(2)证明过程见解析
【解析】分析:(1)先确定p,再设直线方程,与抛物线联立,根据判别式大于零解得直线l的斜率的取值范围,最后根据PA,PB与y轴相交,舍去k=3,(2)先设A(x1,y1),B(x2,y2),与抛物线联立,根据韦达定理可得![]() ,
,![]() .再由
.再由![]() ,
,![]() 得
得![]() ,
,![]() .利用直线PA,PB的方程分别得点M,N的纵坐标,代入化简
.利用直线PA,PB的方程分别得点M,N的纵坐标,代入化简![]() 可得结论.
可得结论.
详解:解:(Ⅰ)因为抛物线y2=2px经过点P(1,2),
所以4=2p,解得p=2,所以抛物线的方程为y2=4x.
由题意可知直线l的斜率存在且不为0,
设直线l的方程为y=kx+1(k≠0).
由![]() 得
得![]() .
.
依题意![]() ,解得k<0或0<k<1.
,解得k<0或0<k<1.
又PA,PB与y轴相交,故直线l不过点(1,-2).从而k≠-3.
所以直线l斜率的取值范围是(-∞,-3)∪(-3,0)∪(0,1).
(Ⅱ)设A(x1,y1),B(x2,y2).
由(I)知![]() ,
,![]() .
.
直线PA的方程为y–2=![]() .
.
令x=0,得点M的纵坐标为![]() .
.
同理得点N的纵坐标为![]() .
.
由![]() ,
,![]() 得
得![]() ,
,![]() .
.
所以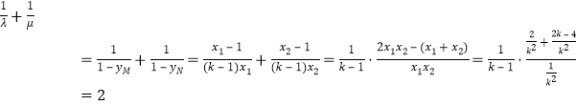 .
.
所以![]() 为定值.
为定值.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】点![]() 为
为![]() 所在的平面内,给出下列关系式:
所在的平面内,给出下列关系式:
①![]() ;
;
② ;
;
③![]() .
.
则点![]() 依次为
依次为![]() 的( )
的( )
A.内心、重心、垂心B.重心、内心、垂心C.重心、内心、外心D.外心、垂心、重心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() ,和两点
,和两点![]() ,给出如下结论其中真命题的序号是________
,给出如下结论其中真命题的序号是________
①当![]() 变化时,
变化时,![]() 与
与![]() 分别经过定点
分别经过定点![]() 和
和![]() ;
;
②不论![]() 为何值时,
为何值时,![]() 与
与![]() 都互相垂直;
都互相垂直;
③如果![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 的最大值是2;
的最大值是2;
④![]() 为直线
为直线![]() 上的点,则
上的点,则![]() 的最小值是
的最小值是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=4sin(2x+![]() )(x∈R),有下列命题:
)(x∈R),有下列命题:
①y=f(x)的表达式可改写为y=4cos(2x﹣![]() );
);
②y=f(x)是以2π为最小正周期的周期函数;
③y=f(x)的图象关于点![]() 对称;
对称;
④y=f(x)的图象关于直线x=﹣![]() 对称.
对称.
其中正确的命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产![]() 产品的年固定成本为250万元,每生产
产品的年固定成本为250万元,每生产![]() 千件需另投人成本
千件需另投人成本![]() 万元.当年产量不足80千件时,
万元.当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() 万元,每千件产品的售价为50万元,该厂生产的产品能全部售完.
万元,每千件产品的售价为50万元,该厂生产的产品能全部售完.
(1)写出年利润![]() 万元关于
万元关于![]() 千件的函数关系式;
千件的函数关系式;
(2)当年产量为多少千件时该厂当年的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com