
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
分析 由$\underset{lim}{h→0}$$\frac{f(2-h)-f(2+h)}{h}$=-($\underset{lim}{h→0}$$\frac{f(2+h)-f(2)}{h}$+$\underset{lim}{h→0}$$\frac{f(2-h)-f(2)}{-h}$)=-f′(2),利用导数的定义,由f′(2)=$\frac{1}{2}$,即可求得答案.
解答 解:由$\underset{lim}{h→0}$$\frac{f(2-h)-f(2+h)}{h}$=-$\underset{lim}{h→0}$$\frac{f(2+h)-f(2-h)}{h}$=-$\underset{lim}{h→0}$$\frac{f(2+h)-f(2)+f(2)-f(2-h)}{h}$=-($\underset{lim}{h→0}$$\frac{f(2+h)-f(2)}{h}$+$\underset{lim}{h→0}$$\frac{f(2-h)-f(2)}{-h}$)=-f′(2),
由f′(2)=$\frac{1}{2}$,则$\underset{lim}{h→0}$$\frac{f(2-h)-f(2+h)}{h}$=-f′(2)=-1,
故选:B.
点评 本题考查极限的运算,考查导数的定义,考查转化思想,属于中档题.


科目:高中数学 来源: 题型:填空题
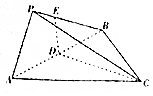 如图所示,三棱锥P-ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA=$\frac{3}{2}$,PB=$\frac{3\sqrt{3}}{2}$,则三棱锥P-ABC的外接球的表面积为13π.
如图所示,三棱锥P-ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA=$\frac{3}{2}$,PB=$\frac{3\sqrt{3}}{2}$,则三棱锥P-ABC的外接球的表面积为13π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=5,b=5,A=50° | B. | a=3,b=4,A=30° | ||
| C. | a=5,b=10,A=30° | D. | a=12,b=10,A=135° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | B⊆A | C. | A∪B=R | D. | A∩B=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 210 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
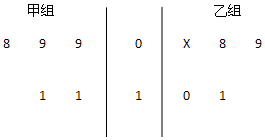 如图茎叶图记录了甲乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示
如图茎叶图记录了甲乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com