
| A. | 外切 | B. | 内切 | C. | 相交 | D. | 内含 |
分析 分别找出圆心坐标和半径,利用两点间的距离公式,求出两圆心的距离d,然后求出R-r,即可得到两圆的位置关系.
解答 解:圆x2+y2+2x+3y+1=0的圆心(-1,-$\frac{3}{2}$),半径为R=$\frac{3}{2}$;
圆x2+y2+4x+3y+2=0化为标准方程得:(x+2)2+(y+$\frac{3}{2}$)2=$\frac{17}{4}$,
故圆心坐标(-2,-$\frac{3}{2}$),半径为r=$\frac{\sqrt{17}}{2}$,
∵圆心之间的距离d=1,$\frac{\sqrt{17}}{2}$-$\frac{3}{2}$<1<$\frac{\sqrt{17}}{2}$+$\frac{3}{2}$
∴两圆的位置关系是相交.
故选:C.
点评 圆与圆的位置关系有五种,分别是:当0≤d<R-r时,两圆内含;当d=R-r时,两圆内切;当R-r<d<R+r时,两圆相交;当d=R+r时,两圆外切;当d>R+r时,两圆外离(其中d表示两圆心间的距离,R,r分别表示两圆的半径).


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.
如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
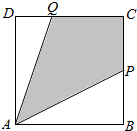 如图,有一块边长为1(百米)的正方形区域ABCD.在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45°(其中点P,Q分别在边BC,CD上),设BP=t.
如图,有一块边长为1(百米)的正方形区域ABCD.在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45°(其中点P,Q分别在边BC,CD上),设BP=t.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com