
【题目】已知:函数![]() ,数列
,数列![]() 对
对![]() ,总有
,总有 ;
;
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() 是数列
是数列![]() 的前
的前![]() 项和,且
项和,且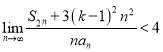 ,求
,求![]() 的取值范围;
的取值范围;
(3)若数列![]() 满足:①
满足:①![]() 为
为![]() 的子数列(即
的子数列(即![]() 中每一项都是
中每一项都是![]() 的项,且按在
的项,且按在![]() 中的顺序排列);②
中的顺序排列);②![]() 为无穷等比数列,它的各项和为
为无穷等比数列,它的各项和为![]() ,这样的数列是否存在?若存在,求出所有符合条件的数列
,这样的数列是否存在?若存在,求出所有符合条件的数列![]() .写出它的通项公式,并证明你的结论;若不存在,说明理由.
.写出它的通项公式,并证明你的结论;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或![]() .
.
【解析】
(1)可证![]() 为等差数列,从而可求其通项.
为等差数列,从而可求其通项.
(2)先求出![]() ,再求出
,再求出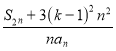 ,化简后利用基本极限可得所求的极限(与
,化简后利用基本极限可得所求的极限(与![]() 有关),解关于
有关),解关于![]() 的不等式后可得所求的范围.
的不等式后可得所求的范围.
(3)先证明无穷等比数列![]() 的公比为
的公比为![]() 且
且![]() 为奇数,再就
为奇数,再就![]() 分类讨论可求
分类讨论可求![]() 的通项.
的通项.
(1)因为 ,故
,故![]() 即
即![]() ,所以
,所以![]() 为等差数列,
为等差数列,
故![]() 即
即![]() .
.
(2)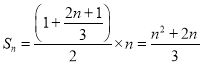 ,
,
所以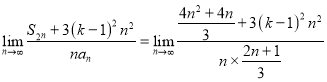
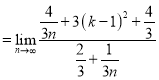 ,
,
因为![]() ,所以
,所以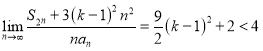 ,
,
所以![]() 即
即![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() .
.
(3)设![]() 的公比为
的公比为![]() 且
且![]() 为互素的奇数,
为互素的奇数,![]() ,
,
则对于任意![]() ,总有
,总有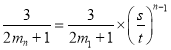 ,
,
所以![]() ,
,
若![]() ,因为
,因为![]() 互素,
互素,![]() 有因数
有因数![]() ,但
,但![]() 为有限数,矛盾, 故
为有限数,矛盾, 故![]() .
.
故公比![]() .
.
当![]() 时,无穷等比数列的各项之和为
时,无穷等比数列的各项之和为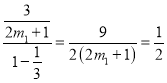 ,故
,故![]() ,
,
此时![]() .
.
当![]() 时,无穷等比数列的各项之和为
时,无穷等比数列的各项之和为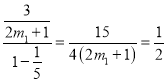 ,故
,故![]() (舍).
(舍).
当![]() 时,无穷等比数列的各项之和为
时,无穷等比数列的各项之和为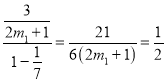 ,故
,故![]() .
.
此时![]() .
.
当![]() 时,无穷等比数列的各项之和为
时,无穷等比数列的各项之和为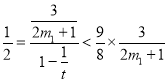 ,故
,故![]() ,
,
所以![]() ,
,
若![]() ,则无穷等比数列的各项之和为
,则无穷等比数列的各项之和为![]() ,舍;
,舍;
若![]() ,则无穷等比数列的各项之和为
,则无穷等比数列的各项之和为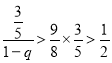 ,舍.
,舍.
综上,所求的无穷等比数列的通项为![]() 后
后![]() .
.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】如图,F1、F2是椭圆C1:![]() +y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是___.
+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是___.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列五个命题:①直线![]() 的斜率
的斜率![]() ,则直线
,则直线![]() 的倾斜角的范围是
的倾斜角的范围是![]() ;②直线
;②直线![]() :
:![]() 与过
与过![]() ,
,![]() 两点的线段相交,则
两点的线段相交,则![]() 或
或![]() ;③如果实数
;③如果实数![]() ,
,![]() 满足方程
满足方程![]() ,那么
,那么![]() 的最大值为
的最大值为![]() ;④直线
;④直线![]() 与椭圆
与椭圆![]() 恒有公共点,则
恒有公共点,则![]() 的取值范围是
的取值范围是![]() ;⑤方程
;⑤方程![]() 表示圆的充要条件是
表示圆的充要条件是![]() 或
或![]() ;正确的是( )
;正确的是( )
A.②③B.③④C.②⑤D.②③⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点![]() ,焦点在
,焦点在![]() 轴上的椭圆,离心率
轴上的椭圆,离心率![]() ,且椭圆过点
,且椭圆过点![]() .
.
(1)求椭圆的方程;
(2)设椭圆左、右焦点分别为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B是焦距为![]() 的椭圆
的椭圆![]()
![]() 的上、下顶点,P是椭圆上异于顶点的任意一点,直线PA,PB的斜率之积为
的上、下顶点,P是椭圆上异于顶点的任意一点,直线PA,PB的斜率之积为![]() .
.
(1)求椭圆的方程;
(2)若C,D分别是椭圆的左、右顶点,动点M满足![]() ,连接CM交椭圆于点E,试问:x轴上是否存在定点T,使得
,连接CM交椭圆于点E,试问:x轴上是否存在定点T,使得![]() 恒成立?若存在,求出点T坐标,若不存在,请说明理由.
恒成立?若存在,求出点T坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直线![]() :
:![]() 和直线
和直线![]() :
:![]() ,射线
,射线![]() 的一个法向量为
的一个法向量为![]() ,点
,点![]() 为坐标原点,且
为坐标原点,且![]() ,直线
,直线![]() 和
和![]() 之间的距离为2,点
之间的距离为2,点![]() ,
,![]() 分别是直线
分别是直线![]() 和
和![]() 上的动点,
上的动点,![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.

(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,
,![]() ,且
,且![]() ,试求
,试求![]() 的最小值;
的最小值;
(3)若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次体育兴趣小组的聚会中,要安排6人的座位,使他们在如图所示的6个椅子中就坐,且相邻座位(如1与2,2与3)上的人要有共同的体育兴趣爱好.现已知这6人的体育兴趣爱好如下表所示,且小林坐在1号位置上,则4号位置上坐的是
小林 | 小方 | 小马 | 小张 | 小李 | 小周 | |
体育兴趣爱好 | 篮球,网球,羽毛球 | 足球,排球,跆拳道 | 篮球,棒球,乒乓球 | 击剑,网球,足球 | 棒球,排球,羽毛球 | 跆拳道,击剑,自行车 |

A.小方B.小张C.小周D.小马
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com