
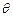 的大小。
的大小。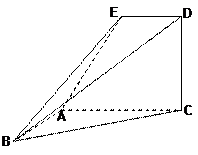
 的中点
的中点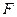 连结
连结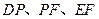 ,则
,则 ,
,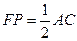 ,
, 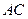 的中点
的中点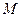 ,连结
,连结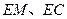 ,
, 且
且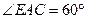 ,
,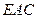 是正三角形,∴
是正三角形,∴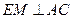 .
.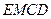 为矩形,∴
为矩形,∴ .又∵
.又∵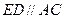 ,
,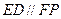 且
且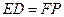 ,四边形
,四边形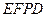 是平行四边形.
是平行四边形.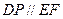 ,而
,而 平面
平面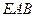 ,
,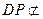 平面
平面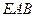 ,∴
,∴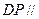 平面
平面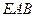 6分
6分
 作
作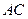 的平行线
的平行线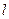 ,过
,过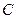 作
作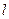 的垂线交
的垂线交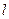 于
于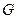 ,连结
,连结 ,
,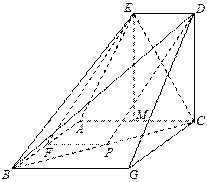
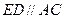 ,∴
,∴ ,
,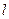 是平面
是平面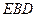 与平面
与平面 所成二面角的棱8分
所成二面角的棱8分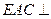 平面
平面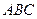 ,
,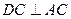 ,∴
,∴ 平面
平面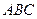 ,
,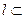 平面
平面 ,
,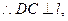 ∴
∴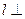 平面
平面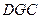 ,∴
,∴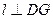 ,
,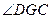 是所求二面角的平面角. 10分
是所求二面角的平面角. 10分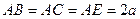 ,则
,则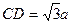 ,
,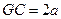 ,
,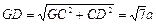 ,
,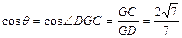 .
. 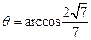 12分
12分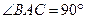 ,平面
,平面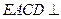 平面
平面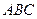 ,
,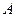 为原点,直线
为原点,直线 为
为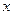 轴,直线
轴,直线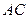 为
为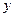 轴,
轴,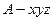 ,则
,则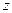 轴在平面
轴在平面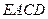 内(如图).
内(如图).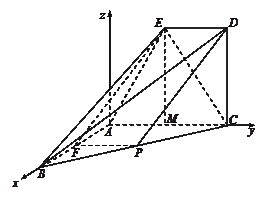
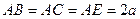 ,由已知,得
,由已知,得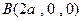 ,
,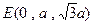 ,
,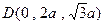 .
. ,
, ,…………………8分
,…………………8分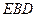 的法向量为
的法向量为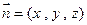 ,
,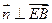 且
且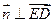 ,
,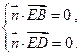 ∴
∴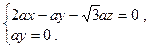 解之得
解之得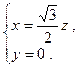
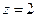 ,得平面
,得平面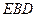 的一个法向量为
的一个法向量为 .
.  的一个法向量为
的一个法向量为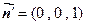 .
.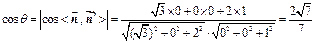 .
. 12分
12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com