
【题目】如图,四棱柱![]() 的底面
的底面![]() 为菱形,且
为菱形,且![]() .
.
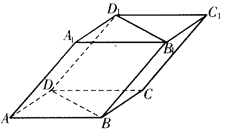
(1)证明:四边形![]() 为矩形;
为矩形;
(2)若![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)由四棱柱性质可知四边形![]() 为平行四边形,连接
为平行四边形,连接![]() ,设
,设![]() ,连接
,连接![]() .,易证∴
.,易证∴![]() 平面
平面![]() ,∴
,∴![]() .∵
.∵![]() ,∴
,∴![]() ; (2) 过点
; (2) 过点![]() 作
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,由已知可得点
,由已知可得点![]() 在
在![]() 上,证明点
上,证明点![]() 与点
与点![]() 重合,则
重合,则![]() 平面
平面![]() ,以
,以![]() 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系![]() 求出平面
求出平面![]() 与平面
与平面![]() 的法向量,代入公式计算即可.
的法向量,代入公式计算即可.
试题解析:
(1)证明:连接![]() ,设
,设![]() ,连接
,连接![]() .
.
∵![]() ,∴
,∴![]() .
.
又![]() 为
为![]() 的中点,∴
的中点,∴![]() ..
..
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
又四边形![]() 是平行四边形,则四边形
是平行四边形,则四边形![]() 为矩形.
为矩形.
(2)解:过点![]() 作
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,由已知可得点
,由已知可得点![]() 在
在![]() 上,∴
上,∴![]() .
.
设![]() ,则
,则![]() .
.
在菱形![]() 中,
中,![]() ,∴
,∴![]() .
.
∴点![]() 与点
与点![]() 重合,则
重合,则![]() 平面
平面![]() .
.
以![]() 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系![]() .
.
则![]() .
.
∴![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则  ,∴
,∴ 即
即![]()
取![]() ,可得
,可得![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
同理可得平面![]() 的一个法向量为
的一个法向量为![]() 。
。
∵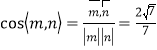 .所以二面角
.所以二面角![]() 的余弦值为
的余弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】从高一年级随机选取100名学生,对他们期中考试的数学和语文成绩进行分析,成绩如图所示.

(Ⅰ)从这100名学生中随机选取一人,求该生数学和语文成绩均低于60分的概率;
(II)从语文成绩大于80分的学生中随机选取两人,记这两人中数学成绩高于80分的人数为![]() ,求
,求![]() 的分布列和数学期望(
的分布列和数学期望(![]() ;
;
(Ill)试判断这100名学生数学成绩的方差![]() 与语文成绩的方差
与语文成绩的方差![]() 的大小.(只需写出结论).
的大小.(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)是奇函数,且满足f(3-x)=f(x),f(-1)=3,数列{an}满足a1=1且an=n(an+1-an)(n∈N*),则f(a36)+f(a37)=( )
A. ![]() B.
B. ![]() C. 2D. 3
C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=nan+n,数列{bn}的前n项和为Tn,求满足不等式![]() 的n的最小值.
的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】襄阳市拟在2021年奥体中心落成后申办2026年湖北省省运会,据了解,目前武汉,宜昌,黄石等申办城市因市民担心赛事费用超支而准备相继退出,某机构为调查襄阳市市民对申办省运会的态度,选取某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 60 | ||
年龄大于50岁 | 10 | ||
合计 | 80 | 100 |
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过![]() 的前提下认为不同年龄与支持申办省运会无关?
的前提下认为不同年龄与支持申办省运会无关?
附: ![]() ,
, ![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() (
(![]() 为大于0的常数).现随机抽取6件合格产品,测得数据如下:
为大于0的常数).现随机抽取6件合格产品,测得数据如下:

对数据作了初步处理,相关统计位的值如下表:

(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现从抽取的6件合格产品中再任选3件,记
内时为优等品.现从抽取的6件合格产品中再任选3件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望.
的分布列和期望.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为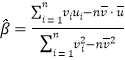 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从高三抽出![]() 名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
名学生参加数学竞赛,由成绩得到如下的频率分布直方图.试利用频率分布直方图求:
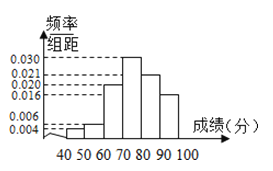
(1)这![]() 名学生成绩的众数与中位数;
名学生成绩的众数与中位数;
(2)这![]() 名学生的平均成绩.
名学生的平均成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究变量![]() ,
,![]() 得到一组样本数据,进行回归分析,有以下结论
得到一组样本数据,进行回归分析,有以下结论
①残差平方和越小的模型,拟合的效果越好;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小说明拟合效果越好;
越小说明拟合效果越好;
③线性回归方程对应的直线![]() 至少经过其样本数据点中的一个点;
至少经过其样本数据点中的一个点;
④若变量![]() 和
和![]() 之间的相关系数为
之间的相关系数为![]() ,则变量
,则变量![]() 和
和![]() 之间的负相关很强.
之间的负相关很强.
以上正确说法的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com