
【题目】已知直线l过点A(2,4),且被平行直线l1:x-y+1=0与l2:x-y-1=0所截的线段中点M在直线x+y-3=0上,求直线l的方程.
【答案】解:解法一:∵点M在直线x+y-3=0上,∴设点M坐标为(t,3-t),由题意知点M到l1 , l2的距离相等,即 ![]() ,解得t=
,解得t= ![]() ,∴
,∴ ![]() .又l过点A(2,4),由两点式得
.又l过点A(2,4),由两点式得 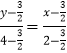 ,
,
即5x-y-6=0,故直线l的方程为5x-y-6=0.
解法二:设与l1 , l2平行且距离相等的直线为l3:x-y+C=0,由两平行直线间的距离公式得 ![]() ,解得C=0,即l3:x-y=0.
,解得C=0,即l3:x-y=0.
由题意得中点M在l3上,又点M在x+y-3=0上.
解方程组 ![]() 得
得 ![]() ∴
∴ ![]() .
.
又l过点A(2,4),故由两点式得直线l的方程为5x-y-6=0
【解析】设出点M的坐标为(t,3-t),结合条件得到关于t的方程,求出t的值,再由两点式得到直线方程.
【考点精析】解答此题的关键在于理解两点式方程的相关知识,掌握直线的两点式方程:已知两点![]() 其中
其中![]() 则:y-y1/y-y2=x-x1/x-x2,以及对点到直线的距离公式的理解,了解点
则:y-y1/y-y2=x-x1/x-x2,以及对点到直线的距离公式的理解,了解点![]() 到直线
到直线![]() 的距离为:
的距离为: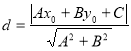 .
.


科目:高中数学 来源: 题型:
【题目】某校初三(1)班、(2)班各有49名学生,两班在一次数学测验中的成绩统计如下表: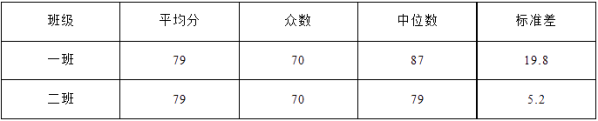
(1)请你对下面的一段话给予简要分析:
高一(1)班的小刚回家对妈妈说:“昨天的数学测验,全班平均分为79分,得70分的人最多,我得了85分,在班里算上上游了!”
(2)请你根据表中的数据,对这两个班的数学测验情况进行简要分析,并提出建议.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ex﹣ax2 , g(x)是f(x)的导函数. (I)求g(x)的极值;
(II)证明:对任意实数x∈R,都有f′(x)≥x﹣2ax+1恒成立:
(Ⅲ)若f(x)≥x+1在x≥0时恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)(ω>0,﹣π<φ<0)在区间 ![]() 上单调递增,且函数值从﹣2增大到0.若
上单调递增,且函数值从﹣2增大到0.若 ![]() ,且f(x1)=f(x2),则f(x1+x2)=( )
,且f(x1)=f(x2),则f(x1+x2)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(1)求曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(2)若当x=﹣1时函数y=g(x)取得极值,确定y=g(x)的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com