
【题目】若椭圆![]() 和椭圆
和椭圆![]() 的焦点相同且
的焦点相同且![]() .给出如下四个结论:
.给出如下四个结论:
①椭圆![]() 与椭圆
与椭圆![]() 一定没有公共点 ②
一定没有公共点 ②![]()
③![]() ④
④![]()
其中所有正确结论的序号是( )
A. ①②③ B. ①③④ C. ①②④ D. ②③④
科目:高中数学 来源: 题型:
【题目】如图所示,△ABC内接于圆O,D是 ![]() 的中点,∠BAC的平分线分别交BC和圆O于点E,F.
的中点,∠BAC的平分线分别交BC和圆O于点E,F. 
(1)求证:BF是△ABE外接圆的切线;
(2)若AB=3,AC=2,求DB2﹣DA2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=![]() 是定义在[-l,1]上的奇函数,且f(
是定义在[-l,1]上的奇函数,且f(![]() )=
)=![]() 。
。
(1)确定函数f(x)的解析式;
(2)判断并用定义证明f(x)在(-1,1)上的单调性;
(3)若f(1-3m)+f(1+m)≥0,求实数m的所有可能的取值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥中P﹣ABCD,AB=BC=CD=DA,∠BAD=60°,AQ=QD,△PAD是正三角形.
(1)求证:AD⊥PB;
(2)已知点M是线段PC上,MC=λPM,且PA∥平面MQB,求实数λ的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 在x=1处取得极值.
在x=1处取得极值.
(1)求函数y=f(x)的单调区间;
(2)当x∈[1,+∞)时,f(x)≥ ![]() 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)当n∈N* , n≥2时,求证:nf(n)<2+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形.
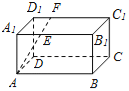
(1)在图中画出这个正方形(不必说明画法和理由);
(2)求直线AF与平面α所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中不正确的是( )
A. 对于线性回归方程![]() ,直线必经过点
,直线必经过点![]()
B. 茎叶图的优点在于它可以保存原始数据,并且可以随时记录
C. 将一组数据中的每一个数据都加上或减去同一常数后,方差恒不变
D. 掷一枚均匀硬币出现正面向上的概率是![]() ,那么一枚硬币投掷2次一定出现正面
,那么一枚硬币投掷2次一定出现正面
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com