
(本小题12分)等差数列 的前
的前 项和记为
项和记为 ,已知
,已知 .
.
(1)求数列 的通项
的通项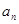 ;(2)若
;(2)若 ,求
,求 ;(3)令
;(3)令 ,求数列
,求数列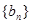 的前
的前 项和
项和 .
.
(1) ;(2)
;(2) ;(3)
;(3)
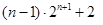
【解析】
试题分析:(1)由 可建立关于a1和d的方程,解出a1和d的值,得到数列
可建立关于a1和d的方程,解出a1和d的值,得到数列 的通项
的通项 .(2)根据
.(2)根据 可建立关于n的方程解出n的值.
可建立关于n的方程解出n的值.
(3)因为 ,显然应采用错位相减的方法求和.
,显然应采用错位相减的方法求和.
(1)由 ,得方程组
,得方程组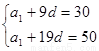 ,
,
解得
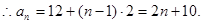 .....................3分
.....................3分
(2)由 得方程
得方程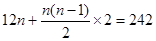
解得 或
或 (舍去),
(舍去),
 .....................6分
.....................6分
(3) .....................7分
.....................7分
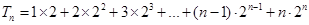
 .....................9分
.....................9分
两式相减得: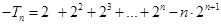 .....................10分
.....................10分

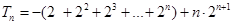
=-
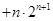 =
=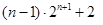 .....................12分
.....................12分
考点:等差数列的通项公式及前n项和公式,以及错位相减法求和.
点评:错位相减法求和主要适应用一个等差数列与一个等比数列对应项的积构成的数列,其前n项和可考虑错位相减法.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:
(本小题满分12分)递增等比数列{an}中a1=2,前n项和为Sn,S2是a2,a3的等差中项:(Ⅰ)求Sn及an;(Ⅱ)数列{bn}满足![]() 的前n项和为Tn,求
的前n项和为Tn,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2011届江西省重点中学协作体高三第二次联考数学理卷 题型:解答题
.(本小题12分)
已知数列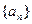 ,
, 分别是等差、等比数列,且
分别是等差、等比数列,且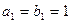 ,
, ,
, .
.
①求数列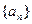 ,
, 的通项公式;
的通项公式;
②设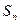 为数列
为数列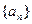 的前
的前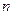 项和,求
项和,求 的前
的前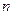 项和
项和 ;
;
③设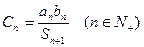 ,
,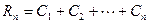 ,请效仿②的求和方法,求
,请效仿②的求和方法,求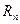 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省协作体高三第二次联考数学理卷 题型:解答题
.(本小题12分)
已知数列 ,
,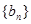 分别是等差、等比数列,且
分别是等差、等比数列,且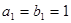 ,
, ,
, .
.
①求数列 ,
,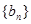 的通项公式;
的通项公式;
②设 为数列
为数列 的前
的前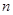 项和,求
项和,求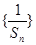 的前
的前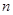 项和
项和 ;
;
③设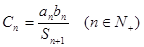 ,
, ,请效仿②的求和方法,求
,请效仿②的求和方法,求 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com