
【题目】已知三棱柱![]() 的底面
的底面![]() 是等边三角形,侧面
是等边三角形,侧面![]() 底面
底面![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 将该三棱柱分成上下两部分的体积比.
将该三棱柱分成上下两部分的体积比.
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”. 其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为![]() ,被平行于这两个平面的任意平面截得的两个截面面积分别为
,被平行于这两个平面的任意平面截得的两个截面面积分别为![]() ,则“
,则“![]() 相等”是“
相等”是“![]() 总相等”的
总相等”的

A. 充分而不必要条件B. 必要而不充分条件
C. 充分必要条件D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,动点
中,动点![]() 到定点
到定点![]() 的距离与
的距离与![]() 到定直线
到定直线![]() 的距离的比为
的距离的比为![]() ,动点
,动点![]() 的轨迹记为
的轨迹记为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若点![]() 在轨迹
在轨迹![]() 上运动,点
上运动,点![]() 在圆
在圆![]() 上运动,且总有
上运动,且总有![]() ,
,
求![]() 的取值范围;
的取值范围;
(3)过点![]() 的动直线
的动直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,试问:在此坐标平面上是否存在一个定点
两点,试问:在此坐标平面上是否存在一个定点![]() ,使得无论
,使得无论![]() 如何转动,以
如何转动,以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标.若不存在,请说明理由.
的坐标.若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间x与乘客等候人数y之间的关系,经过调查得到如下数据:
间隔时间x/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
(1)从这6组数据中随机选取4组数据,求剩下的2组数据的间隔时间相邻的概率;
(2)若选取的是中间4组数据,求y关于x的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”.
,并判断此方程是否是“恰当回归方程”.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: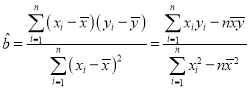 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com