
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,若曲线
,若曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,与
,与![]() 的异于极点的交点为
的异于极点的交点为![]() ,求
,求![]() .
.
科目:高中数学 来源: 题型:
【题目】已知点O为坐标原点,椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,离心率为
(a>b>0)的左、右焦点分别为F1,F2,离心率为![]() ,点I,J分别是椭圆C的右顶点、上顶点,△IOJ的边IJ上的中线长为
,点I,J分别是椭圆C的右顶点、上顶点,△IOJ的边IJ上的中线长为![]() .
.
(1)求椭圆C的标准方程;
(2)过点H(-2,0)的直线交椭圆C于A,B两点,若AF1⊥BF1,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
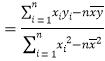 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高血压高血糖和高血脂统称“三高”.如图是西南某地区从2010年至2016年患“三高”人数y(单位:千人)的折线图.
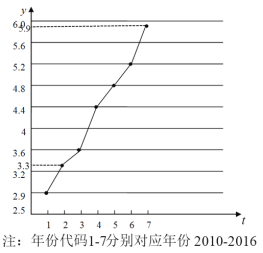
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请求出相关系数(精确到0.01)并加以说明;
的关系,请求出相关系数(精确到0.01)并加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,预测2018年该地区患“三高”的人数.
的回归方程,预测2018年该地区患“三高”的人数.
参考数据:![]() ,
,![]() ,
, ,
,![]() .
.
参考公式:相关系数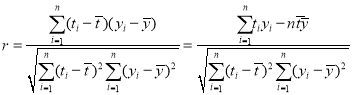 ,
,
回归方程![]() 中:
中: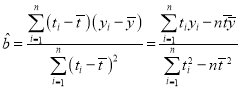 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】雅山中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示.
男 | 女 | |
文科 | 2 | 5 |
理科 | 10 | 3 |
(Ⅰ)若在该样本中从报考文科的学生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(Ⅱ)用假设检验的方法分析有多大的把握认为雅山中学的高三学生选报文理科与性别有关?
参考公式和数据:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种特别列车,沿途共有![]() 个车站(包括起点与终点),因安全需要,规定在同一车站上车的旅客不能在同一车站下车。为了保证上车的旅客都有座位(每位旅客一个座位),则列车至少要安排()个座位。
个车站(包括起点与终点),因安全需要,规定在同一车站上车的旅客不能在同一车站下车。为了保证上车的旅客都有座位(每位旅客一个座位),则列车至少要安排()个座位。
A. ![]() B. 100 C. 110 D. 120
B. 100 C. 110 D. 120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在等比数列{an}中,a1=2,且a1,a2,a3-2成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:![]() ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com