
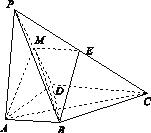
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.

(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
【答案】(1)见解析(2) ![]() (3)
(3) ![]()
【解析】试题分析:(I)以A为坐标原点,建立如图所示的空间直角坐标系,求出BE,DC的方向向量,根据
![]() ,可得BE⊥DC;(II)求出平面PBD的一个法向量,代入向量夹角公式,可得直线BE与平面PBD所成角的正弦值;(Ⅲ)根据BF⊥AC,求出向量
,可得BE⊥DC;(II)求出平面PBD的一个法向量,代入向量夹角公式,可得直线BE与平面PBD所成角的正弦值;(Ⅲ)根据BF⊥AC,求出向量![]() 的坐标,进而求出平面FAB和平面ABP的法向量,代入向量夹角公式,可得二面角F-AB-P的余弦值
的坐标,进而求出平面FAB和平面ABP的法向量,代入向量夹角公式,可得二面角F-AB-P的余弦值
试题解析:方法一:依题意,以点A为原点建立空间直角坐标系(如图所示),可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2).C由E为棱PC的中点,得E(1,1,1).

(1)证明:向量![]() =(0,1,1),
=(0,1,1),![]() =(2,0,0),
=(2,0,0),
故![]() =0,
=0,
所以BE⊥DC.
(2)向量![]() =(-1,2,0),
=(-1,2,0),![]() =(1,0,-2).
=(1,0,-2).
设n=(x,y,z)为平面PBD的法向量,
则
![]()
不妨令y=1,可得n=(2,1,1)为平面PBD的一个法向量.于是有
![]() =
=![]() =
=![]() =
=![]() ,
,
所以直线BE与平面PBD所成角的正弦值为![]() .
.
(3) 向量![]() =(1,2,0),
=(1,2,0),![]() =(-2,-2,2),
=(-2,-2,2),![]() =(2,2,0),
=(2,2,0),![]() =(1,0,0).
=(1,0,0).
由点F在棱PC上,设![]() =λ
=λ![]() ,0≤λ≤1.
,0≤λ≤1.
故![]() =
=![]() +
+![]() =
=![]() +λ
+λ![]() =(1-2λ,2-2λ,2λ).由BF⊥AC,得
=(1-2λ,2-2λ,2λ).由BF⊥AC,得![]() =0,因此2(1-2λ)+2(2-2λ)=0,解得λ=
=0,因此2(1-2λ)+2(2-2λ)=0,解得λ=![]() ,即
,即![]() =
=![]() .设n1=(x,y,z)为平面FAB的法向量,
.设n1=(x,y,z)为平面FAB的法向量,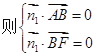 即
即 不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量.取平面ABP的法向量n2=(0,1,0),则
不妨令z=1,可得n1=(0,-3,1)为平面FAB的一个法向量.取平面ABP的法向量n2=(0,1,0),则
cos〈n1,n2〉=![]() =
=![]() =-
=-![]() .
.
易知二面角F AB P是锐角,所以其余弦值为![]() .
.
方法二:(1)证明:如图所示,取PD中点M,连接EM,AM.由于E,M分别为PC,PD的中点,故EM∥DC,且EM=![]() DC.又由已知,可得EM∥AB且EM=AB,故四边形ABEM为平行四边形,所以BE∥AM.
DC.又由已知,可得EM∥AB且EM=AB,故四边形ABEM为平行四边形,所以BE∥AM.
因为PA⊥底面ABCD,故PA⊥CD,而CD⊥DA,从而CD⊥平面PAD.因为AM平面PAD,所以CD⊥AM.又BE∥AM,所以BE⊥CD.
(2)连接BM,由(1)有CD⊥平面PAD,得CD⊥PD.而EM∥CD,故PD⊥EM.又因为AD=AP,M为PD的中点,所以PD⊥AM,可得PD⊥BE,所以PD⊥平面BEM,故平面BEM⊥平面PBD,所以直线BE在平面PBD内的射影为直线BM.而BE⊥EM,可得∠EBM为锐角,故∠EBM为直线BE与平面PBD所成的角.
依题意,有PD=2![]() ,而M为PD中点,可得AM=
,而M为PD中点,可得AM=![]() ,进而BE=
,进而BE=![]() .故在直角三角形BEM中,tan∠EBM=
.故在直角三角形BEM中,tan∠EBM=![]() =
=![]() =
=![]() ,因此sin∠EBM=
,因此sin∠EBM=![]() ,
,
所以直线BE与平面PBD所成角的正弦值为![]() .
.
(3)如图所示,在△PAC中,过点F作FH∥PA交AC于点H.因为PA⊥底面ABCD,所以FH⊥底面ABCD,从而FH⊥AC.又BF⊥AC,得AC⊥平面FHB,因此AC⊥BH.在底面ABCD内,可得CH=3HA,从而CF=3FP.在平面PDC内,作FG∥DC交PD于点G,于是DG=3GP.由于DC∥AB,故GF∥AB,所以A,B,F,G四点共面.由AB⊥PA,AB⊥AD,得AB⊥平面PAD,故AB⊥AG,所以∠PAG为二面角F AB P的平面角.
在△PAG中,PA=2,PG=![]() PD=
PD=![]() ,∠APG=45°.由余弦定理可得AG=
,∠APG=45°.由余弦定理可得AG=![]() ,cos∠PAG=
,cos∠PAG=![]() ,所以二面角F AB P的余弦值为
,所以二面角F AB P的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】设集合A={x|x2﹣3x+2=0},B={x|x2+2(a﹣1)x+(a2﹣5)=0}
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() 分别交
分别交![]() 于
于![]() 两点,交
两点,交![]() 的准线于
的准线于![]() 两点.
两点.
(1)若![]() 在线段
在线段![]() 上,
上, ![]() 是
是![]() 的中点,证明:
的中点,证明: ![]() ;
;
(2)若![]() 的面积是
的面积是![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市“网约车”的现行计价标准是:路程在![]() 以内(含
以内(含![]() )按起步价
)按起步价![]() 元收取,超过
元收取,超过![]() 后的路程按
后的路程按![]() 元/
元/![]() 收取,但超过
收取,但超过![]() 后的路程需加收
后的路程需加收![]() 的返空费(即单
的返空费(即单
价为![]() 元/
元/![]() ).
).
(1) 将某乘客搭乘一次“网约车”的费用![]() (单位:元)表示为行程
(单位:元)表示为行程![]() ,
,
单位:![]() )的分段函数;
)的分段函数;
(2) 某乘客的行程为![]() ,他准备先乘一辆“网约车”行驶
,他准备先乘一辆“网约车”行驶![]() 后,再换乘另一辆
后,再换乘另一辆
“网约车”完成余下行程,请问:他这样做是否比只乘一辆“网约车”完成全部行程更省钱?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求过点P(2,3),且在两坐标轴上的截距相等的直线方程.
(2)已知直线l平行于直线4x+3y-7=0,直线l与两坐标轴围成的三角形的周长是15,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2+bx+c,且f(1)=-![]() ,3a>2c>2b,求证:
,3a>2c>2b,求证:
(1)a>0,且-3<![]() <-
<-![]() ;
;
(2)函数f(x)在区间(0,2)内至少有一个零点;
(3)设x1,x2是函数f(x)的两个零点,则![]() ≤|x1-x2|<
≤|x1-x2|<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ![]() ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点. 
(Ⅰ)求证AM∥平面BDE;
(Ⅱ)求二面角A﹣DF﹣B的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com