
【题目】近年来,我国大力发展新能源汽车工业,新能源汽车(含电动汽车)销量已跃居全球首位.某电动汽车厂新开发了一款电动汽车,并对该电动汽车的电池使用情况进行了测试,其中剩余电量![]() 与行驶时间
与行驶时间![]() (单位:小时)的测试数据如下:
(单位:小时)的测试数据如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
如果剩余电量不足![]() ,则电池就需要充电.
,则电池就需要充电.
(1)从![]() 组数据中选出
组数据中选出![]() 组作回归分析,设
组作回归分析,设![]() 表示需要充电的数据组数,求
表示需要充电的数据组数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)根据电池放电的特点,剩余电量![]() 与时间
与时间![]() 工满足经验关系式:
工满足经验关系式:![]() ,通过散点图可以发现
,通过散点图可以发现![]() 与
与![]() 之间具有相关性.设
之间具有相关性.设![]() ,利用表格中的前
,利用表格中的前![]() 组数据求相关系数
组数据求相关系数![]()
![]() 的把握认为
的把握认为![]() 与
与![]() 之间具有线性相关关系.(当相关系数
之间具有线性相关关系.(当相关系数![]() 满足
满足![]() 时,则认为
时,则认为![]() 的把握认为两个变量具有线性相关关系);
的把握认为两个变量具有线性相关关系);
(3)利用![]() 与
与![]() 的相关性及前
的相关性及前![]() 组数据求出
组数据求出![]() 与工的回归方程.(结果保留两位小数)
与工的回归方程.(结果保留两位小数)
附录:相关数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
前9组数据的一些相关量:
|
|
|
|
|
|
|
|
|
合计 |
|
|
|
|
|
|
|
|
相关公式:对于样本![]() .其回归直线
.其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: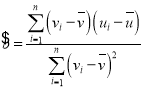 ,
,![]() ,相关系数
,相关系数 .
.
【答案】(1)见解析;(2)有![]() 的把握认为
的把握认为![]() 与
与![]() 之间具有线性相关关系;
之间具有线性相关关系;
(3)![]() .
.
【解析】
(1)根据题知随机变量![]() 的可能取值为
的可能取值为![]() 、
、![]() ,利用古典概型概率公式计算出
,利用古典概型概率公式计算出![]() 和
和![]() 时的概率,可列出随机变量
时的概率,可列出随机变量![]() 的分布列,由数学期望公式可计算出
的分布列,由数学期望公式可计算出![]() ;
;
(2)根据相关系数公式计算出相关系数![]() 的值,结合题中条件说明由
的值,结合题中条件说明由![]() 的把握认为变量
的把握认为变量![]() 与变量
与变量![]() 有线性相关关系;
有线性相关关系;
(3)对![]() 两边取自然对数得出
两边取自然对数得出![]() ,设
,设![]() ,由
,由![]() ,可得出
,可得出![]() ,利用最小二乘法计算出
,利用最小二乘法计算出![]() 关于
关于![]() 的回归直线方程,进而得出
的回归直线方程,进而得出![]() 关于
关于![]() 的回归方程.
的回归方程.
(1)![]() 组数据中需要充电的数据组数为
组数据中需要充电的数据组数为![]() 组.
组.![]() 的所有可能取值为
的所有可能取值为![]() 、
、![]() .
.
![]() ,
,![]() .
.
![]() 的分布列如下:
的分布列如下:
|
|
|
|
|
|
![]() ;
;
(2)由题意知 ,
,
![]() ,
,![]() 有
有![]() 的把握认为
的把握认为![]() 与
与![]() 之间具有线性相关关系;
之间具有线性相关关系;
(3)对![]() 两边取对数得
两边取对数得![]() ,
,
设![]() ,又
,又![]() ,则
,则![]() ,
,
 ,易知
,易知![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() 所求的回归方程为
所求的回归方程为![]() ,即
,即![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 和抛物线
和抛物线![]() ,圆
,圆![]() 与抛物线
与抛物线![]() 的准线交于
的准线交于![]() 、
、![]() 两点,
两点,![]() 的面积为
的面积为![]() ,其中
,其中![]() 是
是![]() 的焦点.
的焦点.
(1)求抛物线![]() 的方程;
的方程;
(2)不过原点![]() 的动直线
的动直线![]() 交该抛物线于
交该抛物线于![]() ,
,![]() 两点,且满足
两点,且满足![]() ,设点
,设点![]() 为圆
为圆![]() 上任意一动点,求当动点
上任意一动点,求当动点![]() 到直线
到直线![]() 的距离最大时直线
的距离最大时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了估计某自然保护区中天鹅的数量,可以使用以下方法:先从该保护区中捕出一定数量的天鹅,例如200只,给每只天鹅做上不影响其存活的记号,然后放回保护区,经过适当的时间,让其和保护区中其余的天鹅充分混合,再从保护区中捕出一定数量的天鹅,例如150只,查看其中有记号的天鹅,设有20只,试根据上述数据,估计该自然保护区中天鹅的数量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是甲、乙两名射击运动员在参赛前的训练中击中10环以上的次数统计,根据表格中的数据回答以下问题:
射击次数 | 10 | 20 | 50 | 100 | 200 | 500 |
甲击中10环以上的次数 | 9 | 17 | 44 | 92 | 179 | 450 |
甲击中10环以上的频率 |
射击次数 | 10 | 20 | 50 | 100 | 200 | 500 |
乙击中10环以上的次数 | 8 | 19 | 44 | 93 | 177 | 453 |
乙击中10环以上的频率 |
(1)分别计算出两位运动员击中10环以上的频率;
(2)根据(l)中的计算结果预测两位运动员在比赛时击中10环以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装,每件服装的成本为40元,出厂单价为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元,根据市场调查,销售商一次订购量不会超过500件.
(1)设一次订购量为x件,服装的实际出厂单价为P元,写出函数![]() 的表达式;
的表达式;
(2)当销售商一次订购450件服装时,该服装厂获得的利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com