
【题目】已知函数f(x)=x2+2aln x.
(1)当a=1时,求函数f′(x)的最小值;
(2)求函数f(x)的单调区间和极值.
【答案】(1)4.
(2) 函数f(x)的单调递减区间是(0,![]() ),单调递增区间是(
),单调递增区间是(![]() ,+∞).函数f(x)有极小值f(
,+∞).函数f(x)有极小值f(![]() )=-a+2aln
)=-a+2aln![]() .
.
【解析】分析:首先求出函数的定义域,先保证函数的生存权,对于第一问,对函数求导,之后应用基本不等式求出![]() 的最小值,注意等号成立的条件;对于第二问求导,之后对参数的取值进行讨论,利用导数大于零,函数单调增,导数小于零,函数单调减,从而确定出函数的单调区间以及函数的极值.
的最小值,注意等号成立的条件;对于第二问求导,之后对参数的取值进行讨论,利用导数大于零,函数单调增,导数小于零,函数单调减,从而确定出函数的单调区间以及函数的极值.
详解:函数f(x)的定义域为(0,+∞).
(1)当a=1时,f′(x)=2x+![]() ≥2
≥2![]() =4,当且仅当2x=
=4,当且仅当2x=![]() ,
,
即x=1时等号成立,故函数f′(x)的最小值为4.
(2)f′(x)=2x+![]() =2(x+
=2(x+![]() ).
).
①当a≥0时,f′(x)>0,因此f(x)的单调递增区间为(0,+∞),这时函数无极值;
②当a<0时,f′(x)=![]() .当x变化时,f′(x),f(x)的变化情况如下:
.当x变化时,f′(x),f(x)的变化情况如下:
x | (0, |
| ( |
f′(x) | - | 0 | + |
f(x) | 减 | 极小值 | 增 |
因此函数f(x)的单调递减区间是(0,![]() ),单调递增区间是(
),单调递增区间是(![]() ,+∞).且当x=
,+∞).且当x=![]() 时,函数f(x)有极小值f(
时,函数f(x)有极小值f(![]() )=-a+2aln
)=-a+2aln![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x+alnx(a>0).
(Ⅰ)当a=2时,试求函数图线过点(1,f(1))的切线方程;
(Ⅱ)当a=1时,若关于x的方程f(x)=x+b有唯一实数解,试求实数b的取值范围;
(Ⅲ)若函数f(x)有两个极值点x1、x2(x1<x2),且不等式f(x1)≥mx2恒成立,试求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,动点
,动点![]() 在直线
在直线![]() :
:![]() 上(
上(![]() ),过
),过![]() 分别作圆
分别作圆![]() ,
,![]() 的切线,切点分别为
的切线,切点分别为![]() ,
,![]() ,若满足
,若满足![]() 的点
的点![]() 有且只有一个,则实数
有且只有一个,则实数![]() 的值为______.
的值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,等腰梯形ABCD的底角A等于60°.直角梯形ADEF所在的平面垂直于平面 ABCD,∠EDA=90°,且ED=AD=2AF=2AB=2.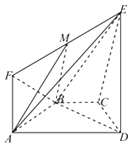
(Ⅰ)证明:平面ABE⊥平面EBD;
(Ⅱ)点M在线段EF上,试确定点M的位置,使平面MAB与平面ECD所成的角的余弦值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
直线![]() 的参数方程为
的参数方程为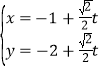 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)已知![]() ,设点
,设点![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于下列说法正确的是( )
A.若f(x)是奇函数,则f(x)是单调函数
B.命题“若x2﹣x﹣2=0,则x=1”的逆否命题是“若x≠1,则x2﹣x﹣2=0”
C.命题p:?x∈R,2x>1024,则¬p:?x0∈R, ![]()
D.命题“?x∈(﹣∞,0),2x<x2”是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在直角坐标系xOy中,设倾斜角为α的直线l:![]() (t为参数)与曲线C:
(t为参数)与曲线C:![]() (θ为参数)相交于不同的两点A,B.
(θ为参数)相交于不同的两点A,B.
(Ⅰ)若α=![]() ,求线段AB中点M的坐标;
,求线段AB中点M的坐标;
(Ⅱ)若|PA|·|PB|=|OP|![]() ,其中P(2,
,其中P(2,![]() ),求直线l的斜率.
),求直线l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
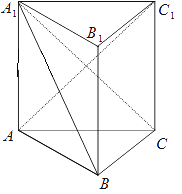
【题目】如图,三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AA1=AC=2BC,∠ACB=90°.
(Ⅰ)求证:AC1⊥A1B;
(Ⅱ)求直线AB与平面A1BC所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,直线l的极坐标方程为ρcos(θ+ ![]() )=1.以极点O为原点,极轴为x轴的正半轴建立平面直角坐标系,圆C的参数方程为
)=1.以极点O为原点,极轴为x轴的正半轴建立平面直角坐标系,圆C的参数方程为 ![]() (θ为参数).若直线l与圆C相切,求r的值.
(θ为参数).若直线l与圆C相切,求r的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com