
【题目】已知无穷数列![]() 的首项
的首项![]() ,
, 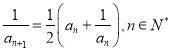 .
.
(Ⅰ)证明: ![]() ;
;
(Ⅱ) 记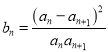 ,
, ![]() 为数列
为数列![]() 的前
的前![]() 项和,证明:对任意正整数
项和,证明:对任意正整数![]() ,
, ![]() .
.
科目:高中数学 来源: 题型:
【题目】给出下列三个命题
①若“p或q”为假命题,则p,q均为真命题;
②命题“若x≥2且y≥3,则x+y≥5”的逆否命题为假命题;
③在△ABC中,“A>45°”是“sinA> ![]() ”的充要条件,
”的充要条件,
其中正确的命题个数是( )
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上不恒为0的函数,且对于任意的实数a,b满足f(2)=2,f(ab)=af(b)+bf(a),an= ![]() (n∈N*),bn=
(n∈N*),bn= ![]() (n∈N*),给出下列命题:
(n∈N*),给出下列命题:
①f(0)=f(1);
②f(x)为奇函数;
③数列{an}为等差数列;
④数列{bn}为等比数列.
其中正确的命题是 . (写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相北上广深等十余大中城市,一款叫“一度用车”的共享汽车在广州提供的车型是“奇瑞eQ”,每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每天租用共享汽车上下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟) |
|
|
|
|
|
次数 | 8 | 14 | 8 | 8 | 2 |
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为![]() 分钟.
分钟.
(Ⅰ)若李先生上.下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设![]() 是4次使用共享汽车中最优选择的次数,求
是4次使用共享汽车中最优选择的次数,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,a2+a7=﹣23,a3+a8=﹣29.
(1)求数列{an}的通项公式;
(2)设数列{an+bn}是首项为1,公比为c的等比数列,求{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x),f(0)≠0,f(1)=2,当x>0,f(x)>1,且对任意a,b∈R,有f(a+b)=f(a)f(b).
(1)求f(0)的值.
(2)求证:对任意x∈R,都有f(x)>0.
(3)若f(x)在R上为增函数,解不等式f(3﹣2x)>4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)设复数z满足|z|=1,且(3+4i)z为纯虚数,求 ![]() ;
;
(2)已知(2 ![]() ﹣
﹣ ![]() )n的展开式中所有二项式系数之和为64,求展开式的常数项.
)n的展开式中所有二项式系数之和为64,求展开式的常数项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于x∈R,[x]表示不超过x的最整数,如[1.1]=1,[﹣2.1]=﹣3.定义R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0≤x≤ ![]() },则A中所有元素的和为( )
},则A中所有元素的和为( )
A.15
B.19
C.20
D.55
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com