
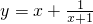 的值域是________.
的值域是________.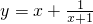 =(x+1)+
=(x+1)+ -1,分x+1>0与x+1<0两种情况讨论,应用基本不等式即可求得函数
-1,分x+1>0与x+1<0两种情况讨论,应用基本不等式即可求得函数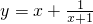 的值域.
的值域.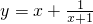 =(x+1)+
=(x+1)+ -1,
-1, -1≥2-1=1,(当且仅当x=0时取“=”);
-1≥2-1=1,(当且仅当x=0时取“=”); ]=-(x+1)-
]=-(x+1)- ≥2,(当且仅当x=-2时取“=”);
≥2,(当且仅当x=-2时取“=”); ≤-2,故y=(x+1)+
≤-2,故y=(x+1)+ -1≤-3;
-1≤-3;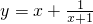 的值域是:(-∞,-3]∪[1,+∞).
的值域是:(-∞,-3]∪[1,+∞).

 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:
 (2012•海淀区二模)某同学为研究函数f(x)=
(2012•海淀区二模)某同学为研究函数f(x)=| 1+x2 |
| 1+(1-x)2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com