
【题目】已知函数f(x)=e|x|+|x|,若关于x的方程f(x)=k有两个不同的实根,则实数k的取值范围是 .
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点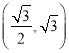 ,离心率为
,离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆的上顶点作直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,
两点, ![]() 为原点.
为原点.
①求证: ![]() ;
;
②设![]() 、
、![]() 分别与椭圆相交于
分别与椭圆相交于![]() 、
、![]() 两点,过原点
两点,过原点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
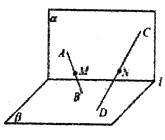
【题目】如图,平面![]() 平面
平面![]() ,
, ![]() 直线
直线![]() ,
, ![]() 是
是![]() 内不同的两点,
内不同的两点, ![]() 是
是![]() 内不同的两点,且
内不同的两点,且![]() 直线
直线![]() 上
上![]() 分别是线段
分别是线段![]() 的中点,下列判断正确的是( )
的中点,下列判断正确的是( )
A. 当![]() 时,
时, ![]() 两点不可能重合
两点不可能重合
B. ![]() 两点可能重合,但此时直线
两点可能重合,但此时直线![]() 与
与![]() 不可能相交
不可能相交
C. 当![]() 与
与![]() 相交,直线
相交,直线![]() 平行于
平行于![]() 时,直线
时,直线![]() 可以与
可以与![]() 相交
相交
D. 当![]() 是异面直线时,直线
是异面直线时,直线![]() 可能与
可能与![]() 平行
平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关结论正确的个数为( )
①小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件![]() =“4个人去的景点不相同”,事件
=“4个人去的景点不相同”,事件![]() “小赵独自去一个景点”,则
“小赵独自去一个景点”,则![]() ;
;
②设函数![]() 存在导数且满足
存在导数且满足![]() ,则曲线
,则曲线![]() 在点
在点![]() 处的切线斜率为-1;
处的切线斜率为-1;
③设随机变量![]() 服从正态分布
服从正态分布![]() ,若
,若![]() ,则
,则![]() 与
与![]() 的值分别为
的值分别为![]() ;
;
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是![]() .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: 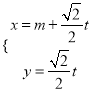 (
(![]() 是参数).
是参数).
(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,将直线![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)若直线l与曲线C相交于A、B两点,且![]() ,试求实数m的值.
,试求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一个居民月用电量标准![]() ,用电量不超过
,用电量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以
的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
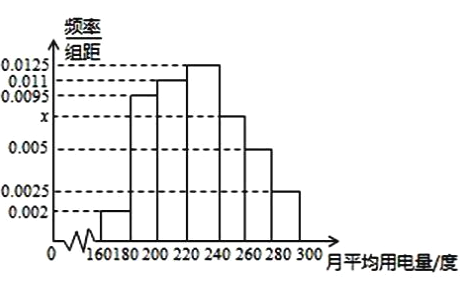
(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)如果当地政府希望使![]() 左右的居民每月的用电量不超出标准,根据样本估计总体的思想,你认为月用电量标准
左右的居民每月的用电量不超出标准,根据样本估计总体的思想,你认为月用电量标准![]() 应该定为多少合理?
应该定为多少合理?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,(a>0).
,(a>0).
(1)当a=2时,证明函数f(x)不是奇函数;
(2)判断函数f(x)的单调性,并利用函数单调性的定义给出证明;
(3)若f(x)是奇函数,且f(x)﹣x2+4x≥m在x∈[﹣2,2]时恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com