
 .
. ,再利用基本不等式即可得到结论.
,再利用基本不等式即可得到结论. ,
, ,得a=b(舍)或
,得a=b(舍)或
 ,∴
,∴
 ,
, 在(0,1)上单调递减,可得
在(0,1)上单调递减,可得
 ,
, 得
得 矛盾
矛盾 在(1,+∞)上单调递增,可得
在(1,+∞)上单调递增,可得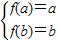 ∴
∴ ,a,b是方程
,a,b是方程 的两个根,此方程无解; …(11分)
的两个根,此方程无解; …(11分)

 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:解答题
 .
. ,若存在,则求出a、b的值;若不存在,请说明理由.
,若存在,则求出a、b的值;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:《第1章 集合与函数概念》2013年单元测试卷5(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省无锡市江阴一中高一(上)第13周数学限时作业(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省南通市如东县双甸高级中学高一(上)9月学情调研数学试卷(解析版) 题型:解答题
 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com