
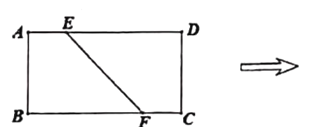
【题目】如图1,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() ,将梯形
,将梯形![]() 沿
沿![]() 折起,使
折起,使![]() 在平面
在平面![]() 上的射影
上的射影![]() 恰好落在线段
恰好落在线段![]() 靠近
靠近![]() 的三等分点处,得到图2中的立体图形.
的三等分点处,得到图2中的立体图形.
(1) (2)
(2) 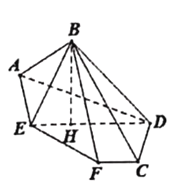
(1)在图2中,求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】在古装电视剧《知否》中,甲乙两人进行一种投壶比赛,比赛投中得分情况分“有初”“贯耳”“散射”“双耳”“依竿”五种,其中“有初”算“两筹”,“贯耳”算“四筹”,“散射”算“五筹”,“双耳”算“六筹”,“依竿”算“十筹”,三场比赛得筹数最多者获胜.假设甲投中“有初”的概率为![]() ,投中“贯耳”的概率为
,投中“贯耳”的概率为![]() ,投中“散射”的概率为
,投中“散射”的概率为![]() ,投中“双耳”的概率为
,投中“双耳”的概率为![]() ,投中“依竿”的概率为
,投中“依竿”的概率为![]() ,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() ,
,![]() 是矩形,
是矩形,![]() ,且平面
,且平面![]() 平面
平面![]() ,
,![]() 点在线段
点在线段![]() 上移动(
上移动(![]() 不与
不与![]() 重合),
重合),![]() 是
是![]() 的中点.
的中点.
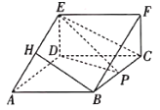
(1)当四面体![]() 的外接球的表面积为
的外接球的表面积为![]() 时,证明:
时,证明:![]() .平面
.平面![]()
(2)当四面体![]() 的体积最大时,求平面
的体积最大时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
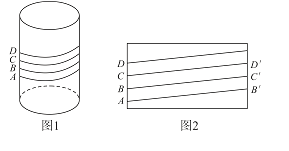
【题目】北方的冬天户外冰天雪地,若水管裸露在外,则管内的水就会结冰从而冻裂水管,给用户生活带来不便.每年冬天来临前,工作人员就会给裸露在外的水管“保暖”:在水管外面包裹保温带,用一条保温带盘旋而上一次包裹到位.某工作人员采用四层包裹法(除水管两端外包裹水管的保温带都是四层):如图1所示是相邻四层保温带的下边缘轮廓线,相邻两条轮廓线的间距是带宽的四分之一.设水管的直径与保温带的宽度都为4cm.在图2水管的侧面展开图中,此保温带的轮廓线与水管母线所成的角的余弦值是( )(保温带厚度忽略不计)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最,编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”,见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注,还得到了无数外国人的关注.某单位有10位外国人,其中关注此次大阅兵的有8位,若从这10位外国人中任意选取3位做一次采访,则被采访者中至少有2位关注此次大阅兵的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级有男生![]() 人,学号为
人,学号为![]() ,
,![]() ,
,![]() ,
,![]() ;女生
;女生![]() 人,学号为
人,学号为![]() ,
,![]() ,
,![]() ,
,![]() .对高三学生进行问卷调查,按学号采用系统抽样的方法,从这
.对高三学生进行问卷调查,按学号采用系统抽样的方法,从这![]() 名学生中抽取
名学生中抽取![]() 人进行问卷调查(第一组采用简单随机抽样,抽到的号码为
人进行问卷调查(第一组采用简单随机抽样,抽到的号码为![]() );再从这
);再从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人进行数据分析,则这
人进行数据分析,则这![]() 人中既有男生又有女生的概率是( )
人中既有男生又有女生的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为( )(注:![]() )
)
A.1624B.1024C.1198D.1560
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com