练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，边长为an的一组正三角形AnBn﹣1Bn的底边Bn﹣1Bn依次排列在x轴上（B0与坐标原点重合）．设{an}是首项为a，公差为2的等差数列，若所有正三角形顶点An在第一象限，且均落在抛物线y2=2px（p＞0）上，则a的值为 ．

    【答案】2
    【解析】解：由题意可得：{an}是首项为a，公差为2的等差数列， ∴an=a+2（n﹣1）．
    ∴a1=a=OB1 ， ∵△A1B0B1是等边三角形，∴ = ， = a．
    同理可得：B1B2=a2=a+2， =a+ = ， = ．
    A1 ，A2 ，
    ∴ =2p× ， =2p× ，
    解得a=2，p= ．
    所以答案是：2．
    【考点精析】根据题目的已知条件，利用等差数列的通项公式（及其变式）的相关知识可以得到问题的答案，需要掌握通项公式：或．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】等差数列{an}满足：a1=1，a2+a6=14；正项等比数列{bn}满足：b1=2，b3=8．
    （Ⅰ） 求数列{an}，{bn}的通项公式an ， bn；
    （Ⅱ）求数列{anbn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，ABCD是正方形，PD⊥平面ABCD，PD=AB=2，E，F，G分别是PC，PD，BC的中点．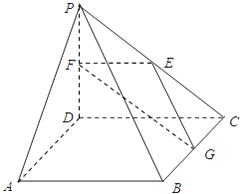

    （1）求证：平面PAB∥平面EFG；
    （2）在线段PB上确定一点Q，使PC⊥平面ADQ，并给出证明；
    （3）求出D到平面EFG的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正三棱柱ABC﹣A1B1C1中，已知AB=CC1=2，则异面直线AB1和BC1所成角的余弦值为（ ）
    A.0
    B.
    C.﹣
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数.

    （I）函数在点处的切线与直线垂直，求a的值；

    （II）讨论函数的单调性；

    （III）不等式在区间上恒成立，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= （x∈R）
    （1）用定义证明f（x）是增函数；
    （2）若g（x）=f（x）﹣a是奇函数，求g（x）在（﹣∞，a]上的取值集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有一个关于平面图形的命题：如图，同一个平面内有两个边长都是a的正方形，其中一个的某顶点在另一个的中心，则这两个正方形重叠部分的面积恒为 ．类比到空间，有两个棱长均为a的正方体，其中一个的某顶点在另一个的中心，则这两个正方体重叠部分的体积恒为 ．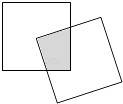

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）

    某学校简单随机抽样方法抽取了100名同学，对其日均课外阅读时间：（单位：分钟）进行调查，结果如下：

    若将日均课外阅读时间不低于60分钟的学生称为“读书迷”

    （1）将频率视为概率，估计该校4000名学生中“读书迷”有多少人？

    （2）从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动．

    ①求抽取的4为同学中有男同学又有女同学的概率；

    ②记抽取的“读书迷”中男生人数为X，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义域为R的函数f（x）= 是奇函数．
    （Ⅰ）求a，b的值；
    （Ⅱ）若对任意的t∈R，不等式f（t2﹣2t）+f（2t2﹣k）＜0恒成立，求k的取值范围．

    查看答案和解析>>

    同步练习册答案