
【题目】要得到![]() 的图象
的图象![]() ,只要将
,只要将![]() 图象
图象![]() 怎样变化得到( )
怎样变化得到( )
A.将![]() 的图象
的图象![]() 沿x轴方向向左平移
沿x轴方向向左平移![]() 个单位
个单位
B.将![]() 的图象
的图象![]() 沿x轴方向向右平移
沿x轴方向向右平移![]() 个单位
个单位
C.先作![]() 关于x轴对称图象
关于x轴对称图象![]() ,再将图象
,再将图象![]() 沿x轴方向向右平移
沿x轴方向向右平移![]() 个单位
个单位
D.先作![]() 关于x轴对称图象
关于x轴对称图象![]() ,再将图象
,再将图象![]() 沿x轴方向向左平移
沿x轴方向向左平移![]() 个单位
个单位
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了美化校园,要对校园内某一区域作如下设计,如图,已知![]() ,
,![]() ,
,![]() ,在边BC上选一点P. 沿着AP和CP重新栽种花木,图中阴影部分铺上草坪. AP段栽种花木费用是每米3a元,CP段栽种花木费用是每米2a元,其中a是正常数.设
,在边BC上选一点P. 沿着AP和CP重新栽种花木,图中阴影部分铺上草坪. AP段栽种花木费用是每米3a元,CP段栽种花木费用是每米2a元,其中a是正常数.设![]() .
.
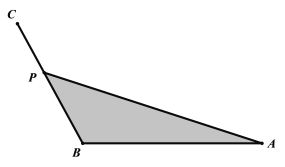
(1)求栽种花木费用y关于θ的函数表达式;
(2)求![]() 的值,使得栽种花木费用y最小.
的值,使得栽种花木费用y最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
在![]() 中,内角A,B,C的对边分别为a,b,c,且满足________________,
中,内角A,B,C的对边分别为a,b,c,且满足________________,![]()
![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 是公差为d(
是公差为d(![]() )的等差数列,它的前n项和记为
)的等差数列,它的前n项和记为![]() ,数列
,数列![]() 是公比为q(
是公比为q(![]() )的等比数列,它的前n项和记为
)的等比数列,它的前n项和记为![]() .若
.若![]() ,且存在不小于3的正整数
,且存在不小于3的正整数![]() ,使
,使![]() .
.
(1)若![]() ,求
,求![]() .
.
(2)若![]() 试比较
试比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(3)若![]() ,是否存在整数m,k,使
,是否存在整数m,k,使![]() 若存在,求出m,k的值;若不存在,说明理由.
若存在,求出m,k的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面为直角梯形,
的底面为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,二面角
,二面角![]() 的大小为
的大小为![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的动点.
上的动点.
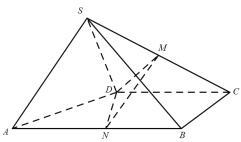
(1)求证:平面![]() 平面
平面![]() ;
;
(2)是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,若存在,求
,若存在,求![]() 的值,不存在说出理由.
的值,不存在说出理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com