
【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)(万元),其中固定成本为3万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)= ![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)甲厂生产多少台新产品时,可使盈利最多?
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(2ax+1)+ ![]() ﹣x2﹣2ax(a∈R).
﹣x2﹣2ax(a∈R).
(1)若x=2为f(x)的极值点,求实数a的值;
(2)若y=f(x)在[3,+∞)上为增函数,求实数a的取值范围;
(3)当a=﹣ ![]() 时,方程f(1﹣x)=
时,方程f(1﹣x)= ![]() 有实根,求实数b的最大值.
有实根,求实数b的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】专家研究表明,![]() 2.5是霾的主要成份,在研究
2.5是霾的主要成份,在研究![]() 2.5形成原因时,某研究人员研究了
2.5形成原因时,某研究人员研究了![]() 2.5与燃烧排放的
2.5与燃烧排放的![]() 、
、![]() 、
、![]() 、
、![]() 等物质的相关关系.下图是某地某月
等物质的相关关系.下图是某地某月![]() 2.5与
2.5与![]() 和
和![]() 相关性的散点图.
相关性的散点图.
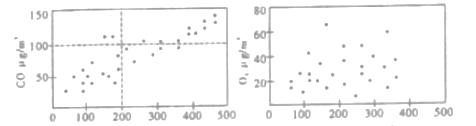
(Ⅰ)根据上面散点图,请你就![]() ,
,![]() 对
对![]() 2.5的影响关系做出初步评价;
2.5的影响关系做出初步评价;
(Ⅱ)根据有关规定,当![]() 排放量低于
排放量低于![]() 时
时![]() 排放量达标,反之为
排放量达标,反之为![]() 排放量超标;当
排放量超标;当![]() 2.5值大于
2.5值大于![]() 时雾霾严重,反之雾霾不严重.根据
时雾霾严重,反之雾霾不严重.根据![]() 2.5与
2.5与![]() 相关性的散点图填写好下面
相关性的散点图填写好下面![]() 列联表,并判断有多大的把握认为“雾霾是否严重与排放量有关”:
列联表,并判断有多大的把握认为“雾霾是否严重与排放量有关”:
雾霾不严重 | 雾霾严重 | 总计 | |
| |||
| |||
总计 |
(Ⅲ)我们知道雾霾对交通影响较大.某市交通部门发现,在一个月内,当![]() 排放量分别是60,120,180时,某路口的交通流量(单位:万辆)一次是800,600,200,而在一个月内,
排放量分别是60,120,180时,某路口的交通流量(单位:万辆)一次是800,600,200,而在一个月内,![]() 排放量是60,120,180的概率一次是
排放量是60,120,180的概率一次是![]() ,
,![]() ,
,![]() (
(![]() ),求该路口一个月的交通流量期望值的取值范围.
),求该路口一个月的交通流量期望值的取值范围.
附:
0.100 | 0.050 | 0.010 | 0.001 | |
2.706 | 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若偶函数f(x)在(﹣∞,﹣1]上是增函数,则下列关系式中成立的是( )
A.f(﹣ ![]() )<f(﹣1)<f(2)
)<f(﹣1)<f(2)
B.f(﹣1)<f(﹣ ![]() )<f(2)??
)<f(2)??
C.f(2)<f(﹣1)<f(﹣ ![]() )
)
D.f(2)<f(﹣ ![]() )<f(﹣1)
)<f(﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:参数方程与极坐标系
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 为倾斜角),以坐标原点O为极点,
为倾斜角),以坐标原点O为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的直角坐标方程,并 求C的焦点F的直角坐标;
的直角坐标方程,并 求C的焦点F的直角坐标;
(2)已知点![]() ,若直线
,若直线![]() 与C相交于A,B两点,且
与C相交于A,B两点,且![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 在平面直角坐标系
在平面直角坐标系![]() 下的参数方程为
下的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的普通方程及极坐标方程;
的普通方程及极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
: ![]() 与曲线
与曲线![]() 交于点
交于点![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列不等关系正确的是( )
A.( ![]() )
) ![]() <34<(
<34<( ![]() )﹣2
)﹣2
B.( ![]() )﹣2<(
)﹣2<( ![]() )
) ![]() <34
<34
C.(2.5)0<( ![]() )2.5<22.5
)2.5<22.5
D.( ![]() )2.5<(2.5)0<22.5
)2.5<(2.5)0<22.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com