
����Ŀ��ijУΪ���ռ�����֪ʶ����ǿѧ���Ļ�����ʶ����ȫУ��֯��һ���йػ���֪ʶ�ľ����������������������ס������������ӣ�ÿ��![]() �ˣ������˾������涨ÿ�˻ش�һ�����⣬���Ϊ����Ӯ��
�ˣ������˾������涨ÿ�˻ش�һ�����⣬���Ϊ����Ӯ��![]() �֣������
�֣������![]() �֣��������ÿ�˴�Եĸ��ʾ�Ϊ
�֣��������ÿ�˴�Եĸ��ʾ�Ϊ![]() ���Ҷ���
���Ҷ���![]() �˴�Եĸ��ʷքeΪ
�˴�Եĸ��ʷքeΪ![]() ���Ҹ��˻ش���ȷ����֮��û��Ӱ�죬��
���Ҹ��˻ش���ȷ����֮��û��Ӱ�죬��![]() ��ʾ�Ҷӵ��ܵ÷֣�
��ʾ�Ҷӵ��ܵ÷֣�
��1����![]() �ķֲ��У�
�ķֲ��У�
��2����ס��������ܵ÷�֮�͵���![]() ���Ҽӻ�ʤ�ĸ��ʣ�
���Ҽӻ�ʤ�ĸ��ʣ�
���𰸡���1���ֲ��м���������2��![]() ��
��
��������
���⣨1��������֪��![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() ���ֱ������Ӧ�ĸ��ʣ��ɴ������
���ֱ������Ӧ�ĸ��ʣ��ɴ������![]() �ķֲ��У���2����
�ķֲ��У���2����![]() ��ʾ���ӵ÷ֵ���
��ʾ���ӵ÷ֵ���![]() �Ҷӵ÷ֵ���
�Ҷӵ÷ֵ���![]() ����
����![]() ��ʾ���ӵ÷ֵ���
��ʾ���ӵ÷ֵ���![]() �Ҷӵ÷ֵ���
�Ҷӵ÷ֵ���![]() ������֪
������֪![]() ��
��![]() ���⣮���û����¼��ĸ��ʼ��㹫ʽ���ɵó��ס��������ܵ÷�֮�͵���
���⣮���û����¼��ĸ��ʼ��㹫ʽ���ɵó��ס��������ܵ÷�֮�͵���![]() ���Ҽӻ�ʤ�ĸ��ʣ�
���Ҽӻ�ʤ�ĸ��ʣ�
�����������1��������֪,![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() �����Ҷ�
�����Ҷ�![]() �˴�Եĸ��ʷֱ�Ϊ
�˴�Եĸ��ʷֱ�Ϊ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() �ķֲ���Ϊ:
�ķֲ���Ϊ:
|
|
|
|
|
|
|
|
|
|
��2����![]() ��ʾ���ӵ÷ֵ���
��ʾ���ӵ÷ֵ���![]() �Ҷӵ÷ֵ���
�Ҷӵ÷ֵ���![]() ��,
��,![]() ��ʾ���ӵ÷ֵ���
��ʾ���ӵ÷ֵ���![]() �Ҷӵ÷ֵ���
�Ҷӵ÷ֵ���![]() ��, ��֪
��, ��֪![]() ����, ��
����, ��![]() ,��ס��������ܵ÷�֮�͵���
,��ס��������ܵ÷�֮�͵���![]() ���Ҽӻ�ʤ�ĸ���Ϊ
���Ҽӻ�ʤ�ĸ���Ϊ![]() ��
��


 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2��������ʽ![]() ���������k��ȡֵ��Χ��
���������k��ȡֵ��Χ��
��3����֤����![]() ʱ������ʽ
ʱ������ʽ![]() ����.
����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ͼ��ͼ��ʾ��������������140�����жϿ�����д���ǣ� ��
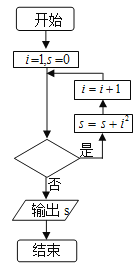
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ĸ����Ϊ��������ǰn���Ϊ
�ĸ����Ϊ��������ǰn���Ϊ![]() ���涨��������
���涨��������![]() ����ǰr�����γɹ���Ϊ1�ĵȲ����У��ӵ�
����ǰr�����γɹ���Ϊ1�ĵȲ����У��ӵ�![]() �����������γɹ���Ϊ2�ĵȱ����У��������
�����������γɹ���Ϊ2�ĵȱ����У��������![]() Ϊ��r�������С���
Ϊ��r�������С���
��1��������![]() Ϊ��6�������С���������
Ϊ��6�������С���������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2���ڣ�1���������£����![]() ����֤����������
����֤����������![]() ��
��![]() ��
��
��3��������![]() Ϊ��6�������С�����
Ϊ��6�������С�����![]() ʱ,��
ʱ,��![]() ��
��![]() ֮�����n������ʹ��
֮�����n������ʹ��![]() �������һ������Ϊ
�������һ������Ϊ![]() �ĵȲ����У���
�ĵȲ����У���![]() ����̽��������
����̽��������![]() ���Ƿ��������
���Ƿ��������![]() ��
��![]() ��
��![]() ����m��k��p�ɵȲ����У��ɵȱ����У������ڣ��������������������ڣ�˵������.
����m��k��p�ɵȲ����У��ɵȱ����У������ڣ��������������������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() ��˫����
��˫����![]() ��һ�������ߣ���
��һ�������ߣ���![]()
![]() ����˫����
����˫����![]() �ϣ�ֱ��
�ϣ�ֱ��![]() ��
��![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ��������ԭ��Ϊ
��������ԭ��Ϊ![]() .
.
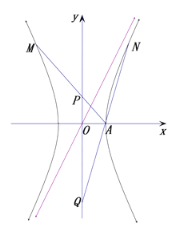
��1����˫����![]() �ķ��̣��������
�ķ��̣��������![]() �����꣨��
�����꣨��![]() ��ʾ����
��ʾ����
��2�����![]() ����
����![]() ��ĶԳƵ�Ϊ
��ĶԳƵ�Ϊ![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() .�ʣ���
.�ʣ���![]() �����Ƿ���ڶ���
�����Ƿ���ڶ���![]() ��ʹ��
��ʹ��![]() �������ڣ������
�������ڣ������![]() �����ꣻ�������ڣ���˵������.
�����ꣻ�������ڣ���˵������.
��3��������![]() ��ֱ��
��ֱ��![]() ��˫����
��˫����![]() ����
����![]() ���㣬��
���㣬��![]() ������ֱ��
������ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼��ij�������һ�������ߵ��������̣����������������ȡһ�������������ߴ�����ݷֳ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �飬�õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.���ߴ���������
�飬�õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.���ߴ���������![]() ֮�⣬����Ϊ������������ϸ��������������
֮�⣬����Ϊ������������ϸ��������������![]() ��
��![]() �ֱ�Ϊ����ƽ���������������ɵ�
�ֱ�Ϊ����ƽ���������������ɵ�![]() ��ͬһ���е������ø���������е�ֵ��������.
��ͬһ���е������ø���������е�ֵ��������.
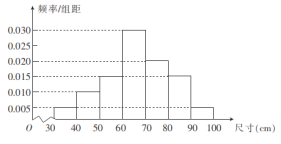
��1����һ������ijߴ���![]() �����жϸ�����Ƿ����������ϸ����������
�����жϸ�����Ƿ����������ϸ����������
��2���������÷ֲ�����ķ�����������ǰ![]() ���г��
���г��![]() ����������ϼǺţ�������
����������ϼǺţ�������![]() ��������ٳ�ȡ
��������ٳ�ȡ![]() �������ٴγ�ȡ��
�������ٴγ�ȡ��![]() �������ǡ��
�������ǡ��![]() ���ߴ�С��
���ߴ�С��![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ������У��������ǣ�������
A.����������ֱ�߶��ཻ������ֱ��������ֱ��
B.����������ֱ�߶��ཻ�ڲ�ͬ�������ֱ��������ֱ��
C.����������ֱ�߶���ֱ��ֱ��������ֱ�ߵĹ�����
D.��![]() ��
��![]() ������ֱ�ߣ�
������ֱ�ߣ�![]() ��
��![]() ������ֱ�ߣ���
������ֱ�ߣ���![]() ��
��![]() ������ֱ��
������ֱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ʵ����![]() �ϵ�ż����
�ϵ�ż����![]() ���溯��
���溯��![]() ����
����![]() ��
��
��1����![]() ��
��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����֤��![]() ������
������![]() �ϵ�������������
�ϵ�������������![]() ������
������![]() �ķ�������
�ķ�������
��3����![]() ������
������![]() ����������
����������![]() ����
����![]() ���������
���������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����|x+1|+2|x��m|
��1����m��2ʱ����f��x����9�Ľ⼯��
��2����f��x����2�Ľ⼯���ǿռ�����ʵ��m��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com