
【题目】已知函数![]() .
.
(1)求![]() 在
在![]() 上的最值;
上的最值;
(2)若![]() ,当
,当![]() 有两个极值点
有两个极值点![]() 时,总有
时,总有![]() ,求此时实数
,求此时实数![]() 的值.
的值.
【答案】(1) 当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
(2) ![]() .
.
【解析】分析:![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上单调递增,即可求解;(2)g′(x)=(x2+2x-1-a)ex,x1+x2=-2,a>-2,x2∈(-1,+∞),g(x2)≤t(2+x1)(ex2+1)(x22-1-a)ex2≤t(2+x1))(ex2+1),-2x2ex2≤t(-x2)(ex2+1),当x2=0时,t∈R;当x2∈(-1,0)时,
上单调递增,即可求解;(2)g′(x)=(x2+2x-1-a)ex,x1+x2=-2,a>-2,x2∈(-1,+∞),g(x2)≤t(2+x1)(ex2+1)(x22-1-a)ex2≤t(2+x1))(ex2+1),-2x2ex2≤t(-x2)(ex2+1),当x2=0时,t∈R;当x2∈(-1,0)时,![]() 恒成立,当x2∈(0,+∞)时,
恒成立,当x2∈(0,+∞)时,![]() 恒成立,综上所述
恒成立,综上所述![]() .
.
详解:
(1)![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴当![]() 时,
时,![]()
当![]() 时,
时,![]()
(2)![]() ,则
,则![]()
根据题意,方程![]() 有两个不同的实根
有两个不同的实根![]() ,
,
所以![]() ,即
,即![]() ,且
,且![]() .由
.由![]() ,
,
可得![]() ,又
,又![]() ,
,
所以上式化为![]() 对任意的
对任意的![]() 恒成立.
恒成立.
(ⅰ)当![]() 时,不等式
时,不等式![]() 恒成立,
恒成立,![]() ;
;
(ⅱ)当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() .
.
令函数![]() ,显然,
,显然,![]() 是
是![]() 上的增函数,
上的增函数,
所以当![]() 时,
时,![]() ,所以
,所以![]() .
.
(ⅲ)当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() .
.
由(ⅱ)得,当![]() 时,
时,![]() ,所以
,所以![]() .
.
综上所述![]() .
.


科目:高中数学 来源: 题型:
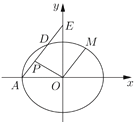
【题目】如图,已知椭圆![]() :
:![]() ,左顶点为
,左顶点为![]() ,经过点
,经过点![]() ,过点
,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为
为![]() 的中点,
的中点,![]() ,证明:对于任意的
,证明:对于任意的![]() 都有
都有![]() 恒成立;
恒成立;
(3)若过点![]() 作直线
作直线![]() 的平行线交椭圆
的平行线交椭圆![]() 于点
于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,椭圆C过点![]() ,两个焦点为
,两个焦点为![]() ,
,![]() ,E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,直线EF的斜率为
,E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,直线EF的斜率为![]() ,直线l与椭圆C相切于点A,斜率为
,直线l与椭圆C相切于点A,斜率为![]() .
.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有![]() 、
、![]() 、
、![]() 、
、![]() 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖,在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖,在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.
甲说:“![]() 、
、![]() 同时获奖.”
同时获奖.”
乙说:“![]() 、
、![]() 不可能同时获奖.”
不可能同时获奖.”
丙说:“![]() 获奖.”
获奖.”
丁说:“![]() 、
、![]() 至少一件获奖”
至少一件获奖”
如果以上四位同学中有且只有两位同学的预测是正确的,则获奖的作品是( )
A. 作品![]() 与作品
与作品![]() B. 作品
B. 作品![]() 与作品
与作品![]() C. 作品
C. 作品![]() 与作品
与作品![]() D. 作品
D. 作品![]() 与作品
与作品![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com