
【题目】某中学某社团为研究高三学生课下钻研数学时间与数学考试中的解答题得分的关系,随机调查了某中学高三某班![]() 名学生每周课下钻研数学时间
名学生每周课下钻研数学时间![]() (单位:小时)与高三下学期期中考试数学解答题得分
(单位:小时)与高三下学期期中考试数学解答题得分![]() ,数据如下表:
,数据如下表:
| 2 | 4 | 6 | 8 | 10 | 12 |
| 30 | 38 | 44 | 48 | 50 | 54 |
(1)根据上述数据,求出数学考试中的解答题得分![]() 与该学生课下钻研数学时间
与该学生课下钻研数学时间![]() 的线性回归方程,并预测某学生每周课下钻研数学时间为
的线性回归方程,并预测某学生每周课下钻研数学时间为![]() 小时其数学考试中的解答题得分;
小时其数学考试中的解答题得分;
(2)从这![]() 人中任选
人中任选![]() 人,求
人,求![]() 人中至少有
人中至少有![]() 人课下钻研数学时间不低于
人课下钻研数学时间不低于![]() 小时的概率.
小时的概率.
参考公式:![]() ,其中
,其中 ,
,![]() ;参考数据:
;参考数据:![]()
【答案】(1)线性回归方程: ![]() ,预测值为:
,预测值为:![]() 分(2)
分(2)![]()
【解析】
(1)先求均值,再代入公式求![]() ,即得线性回归方程;在线性回归方程令
,即得线性回归方程;在线性回归方程令![]() ,解得预测值;
,解得预测值;
(2)利用枚举法确定总基本事件数以及所求事件包含的基本事件数,最后根据古典概型概率公式求结果.
(1)![]()
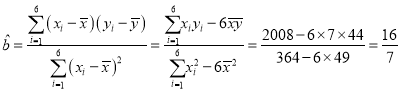
![]()
![]()
当![]() 时,
时,![]()
预测值为:![]() 分
分
(2)设“这2人中至少有一个人刻下钻研数学时间不低于8小时为事件A”
所有基本事件如下:
(2,4),(2,6),(2,8),(2,10),(2,12),(4,6),(4,8),(4,10),(4,12), (6,8),(6,10),(6,12),(8,10),(8,12),(10,12)
共15个基本事件
事件A包含(2,8),(2,10),(2,12),(4,8),(4,10),(4,12),(6,8),(6,10)(6,12),(8,10),(8,12),(10,12)共12个基本事件
所以![]()


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为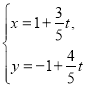 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代著名数学经典,其中对勾股定理的论述,比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小;以锯锯之,深一寸,锯道长一尺,问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺,问这块圆柱形木料的直径是多少?长为0.5丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).己知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌墙内部分的体积约为( )(注:一丈=10尺=100寸,
寸,估算该木材镶嵌墙内部分的体积约为( )(注:一丈=10尺=100寸,![]() )
)
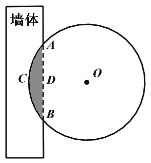
A.300立方寸B.305.6立方寸C.310立方寸D.316.6立方寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代的四书是指:《大学》、《中庸》、《论语》、《孟子》,甲、乙、丙、丁![]() 名同学从中各选一书进行研读,已知四人选取的书恰好互不相同,且甲没有选《中庸》,乙和丙都没有选《论语》,则
名同学从中各选一书进行研读,已知四人选取的书恰好互不相同,且甲没有选《中庸》,乙和丙都没有选《论语》,则![]() 名同学所有可能的选择有______种.
名同学所有可能的选择有______种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com