
【题目】在正三棱柱ABCA1B1C1中,已知AB=1,AA1=2,E,F,G分别是棱AA1,AC和A1C1的中点,以![]() 为正交基底,建立如图所示的空间直角坐标系F-xyz.
为正交基底,建立如图所示的空间直角坐标系F-xyz.

(1)求异面直线AC与BE所成角的余弦值;
(2)求二面角F-BC1-C的余弦值.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)先根据空间直角坐标系,求得向量![]() 和向量
和向量![]() 的坐标,再利用线线角的向量方法求解.
的坐标,再利用线线角的向量方法求解.
(2)分别求得平面BFC1的一个法向量和平面BCC1的一个法向量,再利用面面角的向量方法求解.
规范解答 (1) 因为AB=1,AA1=2,则F(0,0,0),A![]() ,C
,C![]() ,B
,B ,E
,E![]() ,
,
所以![]() =(-1,0,0),
=(-1,0,0),![]() =
=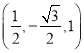
记异面直线AC和BE所成角为α,
则cosα=|cos〈![]() 〉|=
〉|=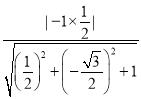 =
=![]() ,
,
所以异面直线AC和BE所成角的余弦值为![]() .
.
(2) 设平面BFC1的法向量为![]() = (x1,y1,z1).
= (x1,y1,z1).
因为![]() =
= ,
,![]() =
=![]() ,
,
则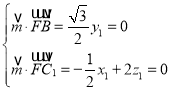
取x1=4,得平面BFC1的一个法向量为![]() =(4,0,1).
=(4,0,1).
设平面BCC1的法向量为![]() =(x2,y2,z2).
=(x2,y2,z2).
因为![]() =
=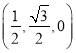 ,
,![]() =(0,0,2),
=(0,0,2),
则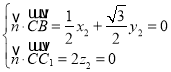
取x2=![]() 得平面BCC1的一个法向量为
得平面BCC1的一个法向量为![]() =(
=(![]() ,-1,0),
,-1,0),
所以cos〈![]() 〉=
〉=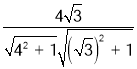 =
=![]()
根据图形可知二面角F-BC1-C为锐二面角,
所以二面角F-BC1-C的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】设椭圆![]()
![]() (
(![]() )的左右顶点为
)的左右顶点为![]() ,上下顶点为
,上下顶点为![]() ,菱形
,菱形![]() 的内切圆
的内切圆![]() 的半径为
的半径为![]() ,椭圆的离心率为
,椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆上关于原点对称的两点,椭圆上一点
是椭圆上关于原点对称的两点,椭圆上一点![]() 满足
满足![]() ,试判断直线
,试判断直线![]() 与圆
与圆![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直线PB与CD所成角的大小为![]() ,求BC的长;
,求BC的长;
(Ⅱ)求二面角B-PD-A的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以正四棱锥VABCD的底面中心O为坐标原点建立空间直角坐标系Oxyz,其中Ox∥BC,Oy∥AB,E为VC的中点.正四棱锥的底面边长为2a,高为h,且有cos〈![]() ,
,![]() 〉=-
〉=-![]() .
.
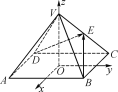
(1)求![]() 的值;
的值;
(2)求二面角B-VC-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某公司一种产品的日销售量![]() (单位:百件)关于日最高气温
(单位:百件)关于日最高气温![]() (单位:
(单位:![]() )的散点图.
)的散点图.

数据:
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
(1)请剔除一组数据,使得剩余数据的线性相关性最强,并用剩余数据求日销售量![]() 关于日最高气温
关于日最高气温![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据现行《重庆市防暑降温措施管理办法》.若气温超过36度,职工可享受高温补贴.已知某日该产品的销售量为53.1,请用(1)中求出的线性回归方程判断该公司员工当天是否可享受高温补贴?
附: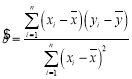 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() 的焦距为
的焦距为![]() ,直线
,直线![]() (
(![]() )与
)与![]() 交于两个不同的点
交于两个不同的点![]() 、
、![]() ,且
,且![]() 时直线
时直线![]() 与
与![]() 的两条渐近线所围成的三角形恰为等边三角形.
的两条渐近线所围成的三角形恰为等边三角形.
(1)求双曲线![]() 的方程;
的方程;
(2)若坐标原点![]() 在以线段
在以线段![]() 为直径的圆的内部,求实数
为直径的圆的内部,求实数![]() 的取值范围;
的取值范围;
(3)设![]() 、
、![]() 分别是
分别是![]() 的左、右两顶点,线段
的左、右两顶点,线段![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:线段
,求证:线段![]() 在
在![]() 轴上的射影长为定值.
轴上的射影长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为![]() 的数列
的数列![]() 各项均为正数,且
各项均为正数,且![]() ,
,![]() .
.
(1)若数列![]() 的通项
的通项![]() 满足
满足![]() ,且
,且![]() ,求数列
,求数列![]() 的前n项和为
的前n项和为![]() ;
;
(2)若数列![]() 的通项
的通项![]() 满足
满足 ,前n项和为
,前n项和为![]() ,当数列
,当数列![]() 是等差数列时,对任意的
是等差数列时,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求满足条件的所有整数
成立,求满足条件的所有整数![]() 构成的集合.
构成的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为椭圆E:
为椭圆E:![]() 的左、右焦点,过点
的左、右焦点,过点![]() 的直线l与椭圆E有且只有一个交点T.
的直线l与椭圆E有且只有一个交点T.
(1)求![]() 面积的取值范围.
面积的取值范围.
(2)若有一束光线从点![]() 射出,射在直线l上的T点上,经过直线l反射后,试问反射光线是否恒过定点?若是,请求出该定点;若否,请说明理由.
射出,射在直线l上的T点上,经过直线l反射后,试问反射光线是否恒过定点?若是,请求出该定点;若否,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com