
【题目】已知![]() 为定义在
为定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,有
时,有![]() ,且当
,且当![]() 时,
时, ![]() ,给出下列命题:
,给出下列命题:
①![]() 的值为
的值为![]() ;②函数
;②函数![]() 在定义域上为周期是2的周期函数;
在定义域上为周期是2的周期函数;
③直线![]() 与函数
与函数![]() 的图像有1个交点;④函数
的图像有1个交点;④函数![]() 的值域为
的值域为![]() .
.
其中正确的命题序号有__________ .
【答案】①③④
【解析】试题分析:根据已知中函数的奇偶性,及当x≥0时,有f(x+1)=﹣f(x),且当x∈[0,1)时,f(x)=log2(x+1),画出函数的图象,逐一分析四个结论的真假,可得答案.
解:∵f(x)为定义在R上的偶函数,
且当x≥0时,有f(x+1)=﹣f(x),
且当x∈[0,1)时,f(x)=log2(x+1),
故函数f(x)的图象如下图所示:

由图可得:f(2013)+f(﹣2014)=0+0=0,故①正确;
函数f(x)在定义域上不是周期函数,故②错误;
直线y=x与函数f(x)的图象有1个交点,故③正确;
函数f(x)的值域为(﹣1,1),故④正确;
故正确的命题序号有:①③④
故答案为:①③④


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】直线l经过两直线l1:2x-y+4=0与l2:x-y+5=0的交点,且与直线x-2y-6=0垂直.
(1)求直线l的方程.
(2)若点P(a,1)到直线l的距离为![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设人的某一特征(如眼睛的大小)是由他的一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:
(1)1个孩子显露显性特征的概率是多少?
(2)“该父母生的2个孩子中至少有1个显露显性特征”,这种说法正确吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x2-2aln x+(a-2)x,a∈R.
x2-2aln x+(a-2)x,a∈R.
(1)当a=1时,求函数f(x)的图象在点(1,f(1))处的切线方程.
(2)是否存在实数a,对任意的x1,x2∈(0,+∞)且x1≠x2有![]() >a恒成立?若存在,求出a的取值范围;若不存在,说明理由.
>a恒成立?若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,求|a+b|和a+b与c的夹角;
(2)设O为△ABC的外心,已知AB=3,AC=4,非零实数x,y满足![]() =x
=x![]() +y
+y![]() ,且x+2y=1,求cos ∠BAC的值.
,且x+2y=1,求cos ∠BAC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学(成绩得分为整数,满分100分)进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在![]() 的人数为12人.
的人数为12人.
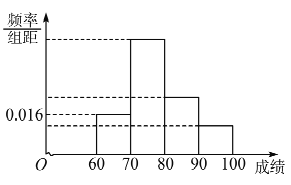
(Ⅰ)求此班级人数;
(Ⅱ)按规定预赛成绩不低于90分的选手参加决赛,已知甲乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.
(i)甲不排在第一位乙不排在最后一位的概率;
(ii)记甲乙二人排在前三位的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com