
【题目】如图,四棱锥P﹣ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(1)求证:平面AEC⊥平面PDB;
(2)当PD=![]() AB,且E为PB的中点时,求AE与平面PDB所成的角的大小.
AB,且E为PB的中点时,求AE与平面PDB所成的角的大小.

【答案】(1)见解析(2)45°.
【解析】本题主要考查了直线与平面垂直的判定,以及直线与平面所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.
(Ⅰ)欲证平面AEC⊥平面PDB,根据面面垂直的判定定理可知在平面AEC内一直线与平面PDB垂直,而根据题意可得AC⊥平面PDB;
(Ⅱ)设AC∩BD=O,连接OE,根据线面所成角的定义可知∠AEO为AE与平面PDB所的角,在Rt△AOE中求出此角即可.
(1)证明:∵底面ABCD是正方形
∴AC⊥BD
又PD⊥底面ABCD
PD⊥AC
(2)解:设AC与BD交于O点,连接EO
则易得∠AEO为AE与面PDB所成的角
∵E、O为中点 ∴EO=![]() PD ∴EO⊥AO
PD ∴EO⊥AO
∴在Rt△AEO中 OE=![]() PD=
PD=![]() AB=AO
AB=AO
∴∠AEO=45° 即AE与面PDB所成角的大小为45°


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取![]() 名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
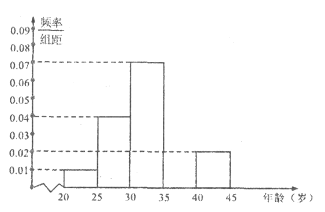
(1)求出表中的![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访,再从抽出的这20名中年龄在![]() 的选取2名担任主要发言人.记这2名主要发言人年龄在
的选取2名担任主要发言人.记这2名主要发言人年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列几个命题:
① 命题![]() 任意
任意![]() ,都有
,都有![]() ,则
,则![]() 存在
存在![]() ,使得
,使得![]() .
.
② 命题“若![]() 且
且![]() ,则
,则![]() 且
且![]() ”的逆命题为假命题.
”的逆命题为假命题.
③ 空间任意一点![]() 和三点
和三点![]() ,则
,则![]() 是
是![]() 三点共线的充分不必要条件.
三点共线的充分不必要条件.
④ 线性回归方程![]() 对应的直线一定经过其样本数据点
对应的直线一定经过其样本数据点![]() 中的一个.
中的一个.
其中不正确的个数为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和记为Sn , a1=1,an+1=2Sn+1(n≥1).
(1)求{an}的通项公式;
(2)等差数列{bn}的各项为正,其前n项和为Tn , 且T3=15,又a1+b1 , a2+b2 , a3+b3成等比数列,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B分别是直线y=x和y=-x上的两个动点,线段AB的长为![]() ,D是AB的中点.
,D是AB的中点.
(1)求动点D的轨迹C的方程;
(2)若过点(1,0)的直线l与曲线C交于不同两点P、Q,当|PQ|=3时,求直线l的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,地面上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高为10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧. 
(1)若圆形标志物半径为25m,以PG所在直线为x轴,G为坐标原点,建立直角坐标系,求圆C和直线PF的方程;
(2)若在点P处观测该圆形标志的最大视角(即∠APF)的正切值为 ![]() ,求该圆形标志物的半径.
,求该圆形标志物的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项的和Sn,点(n,Sn)在函数
的前n项的和Sn,点(n,Sn)在函数![]() =2x2+4x图象上:
=2x2+4x图象上:
(1)证明![]() 是等差数列;
是等差数列;
(2)若函数![]() ,数列{bn}满足bn=
,数列{bn}满足bn=![]() ,记cn=anbn,求数列
,记cn=anbn,求数列![]() 前n项和Tn;
前n项和Tn;
(3)是否存在实数λ,使得当x≤λ时,f(x)=﹣x2+4x﹣![]() ≤0对任意n∈N*恒成立?若存在,求出最大的实数λ,若不存在,说明理由.
≤0对任意n∈N*恒成立?若存在,求出最大的实数λ,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程.
在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() .若点
.若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com