
【题目】小赵和小王约定在早上![]() 至
至![]() 之间到某公交站搭乘公交车去上学,已知在这段时间内,共有
之间到某公交站搭乘公交车去上学,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为
班公交车到达该站,到站的时间分别为![]() ,
,![]() ,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足![]() ,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上方程f(x)-mx-m=0有两个不同的实根,则实数m的取值范围是()
,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上方程f(x)-mx-m=0有两个不同的实根,则实数m的取值范围是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 底面
底面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() 在
在![]() 上,且
上,且![]() 面
面![]() .
.

(1)求证: ![]() 是
是![]() 的中点;
的中点;
(2)在![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 为直角?若存在,求出
为直角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)分别求出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 在曲线
在曲线![]() 上,且
上,且![]() 到直线
到直线![]() 的距离为1,求满足这样条件的点
的距离为1,求满足这样条件的点![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究函数f(x)=![]() (x∈R)时,分别给出下面几个结论:
(x∈R)时,分别给出下面几个结论:
①等式f(-x)=-f(x)在x∈R时恒成立;
②函数f(x)的值域为(-1,1);
③若x1≠x2,则一定有f(x1)≠f(x2);
④方程f(x)=x在R上有三个根.
其中正确结论的序号有______.(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市气象站观测点记录的连续![]() 天里,
天里,![]() 指数(空气质量指数)
指数(空气质量指数)![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位cm)的情况如下表1:
(单位cm)的情况如下表1:
表1
|
|
|
|
|
|
|
|
|
|
该市某月![]() 指数频数分布如下表2:
指数频数分布如下表2:
表2
|
|
|
|
|
|
频数 |
|
|
|
|
|
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(参考公式:![]() ;其中
;其中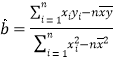 ,
,![]() )
)
(2)小张开了一家洗车店,经统计,当![]() 不高于
不高于![]() 时,洗车店平均每天亏损约
时,洗车店平均每天亏损约![]() 元;当
元;当![]() 在
在![]() 至
至![]() 时,洗车店平均每天收入月
时,洗车店平均每天收入月![]() 元;当
元;当![]() 大于
大于![]() 时,洗车店平均每天收入约
时,洗车店平均每天收入约![]() 元;根据表
元;根据表![]() 估计小张的洗车店该月份平均每天的收入.
估计小张的洗车店该月份平均每天的收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若关于x的不等式ax2﹣3x+2>0(a∈R)的解集为{x|x<1或x>b},求a,b的值;
(2)解关于x的不等式ax2﹣3x+2>5﹣ax(a∈R).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学家门前有一笔直公路直通长城,星期天,他骑自行车匀速前往旅游,他先前进了![]() ,觉得有点累,就休息了一段时间,想想路途遥远,有些泄气,就沿原路返回骑了
,觉得有点累,就休息了一段时间,想想路途遥远,有些泄气,就沿原路返回骑了![]() , 当他记起诗句“不到长城非好汉”,便调转车头继续前进. 则该同学离起点的距离
, 当他记起诗句“不到长城非好汉”,便调转车头继续前进. 则该同学离起点的距离![]() 与时间
与时间![]() 的函数关系的图象大致为( )
的函数关系的图象大致为( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com