
【题目】如图,在四棱锥![]() 中,四边形ABCD是平行四边形,
中,四边形ABCD是平行四边形,![]() ,
,![]() ,
,![]() .
.
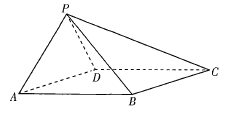
(1)求PC的长;
(2)求AP与平面PBC所成角的正弦值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)取AD的中点E,连接PE,BE,由等边三角形的性质可得![]() ,由勾股定理可得
,由勾股定理可得![]() ,则
,则![]() 平面PBE,即
平面PBE,即![]() ,由平行四边形可得
,由平行四边形可得![]() ,进而求解;
,进而求解;
(2)过点A作平面PBC的垂线,垂足为H,连接PH,则![]() 即AP与平面PBC所成的角,由(1)可得
即AP与平面PBC所成的角,由(1)可得![]() 平面PBE,则
平面PBE,则![]() 平面PBE,即可证得
平面PBE,即可证得![]() 平面PBC,由
平面PBC,由![]() 平面PBC可得
平面PBC可得![]() ,进而利用勾股定理求得
,进而利用勾股定理求得![]() ,即可求解.
,即可求解.
解:(1)如图,取AD的中点E,连接PE,BE,因为![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,
,![]() 平面PBE,所以
平面PBE,所以![]() 平面PBE,
平面PBE,
又![]() 平面PBE,所以
平面PBE,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() .
.
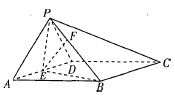
(2)过点A作平面PBC的垂线,垂足为H,连接PH,则![]() 即AP与平面PBC所成的角,
即AP与平面PBC所成的角,
过E作PB的垂线交PB于点F,因为![]() ,
,![]() 平面PBE,
平面PBE,
所以![]() 平面PBE,所以
平面PBE,所以![]() ,
,
又![]() ,
,![]() ,PB,
,PB,![]() 平面PBC,
平面PBC,
所以![]() 平面PBC,
平面PBC,
因为![]() ,所以
,所以![]() 平面PBC,所以
平面PBC,所以![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
因此![]() ,
,
所以 .
.



 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源: 题型:
【题目】已知在四棱柱ABCD—A1B1C1D1中,底面ABCD是菱形,且平面A1ADD1⊥平面ABCD,DA1=DD1,点E,F分别为线段A1D1,BC的中点.
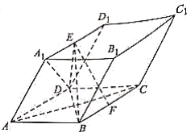
(1)求证:EF∥平面CC1D1D;
(2)求证:AC⊥平面EBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,由于疫情影响,开学延迟,为了不影响学生的学习,国务院、省市区教育行政部门倡导各校开展“停学不停课、停学不停教”,某校语文学科安排学生学习内容包含老师推送文本资料学习和视频资料学习两类,且这两类学习互不影响已知其积分规则如下:每阅读一篇文本资料积1分,每日上限积5分;观看视频1个积2分,每日上限积6分.经过抽样统计发现,文本资料学习积分的概率分布表如表1所示,视频资料学习积分的概率分布表如表2所示.


(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为ξ,求ξ的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海南盛产各种名贵树木,如紫檀、黄花梨等.在实际测量单根原木材体积时,可以检量木材的实际长度(检尺长)和小头直径(检尺径),再通过国家公布的原木材积表直接查询得到,原木材积表的部分数据如下所示:
检尺径 ( | 检尺长( | ||||
2.0 | 2.2 | 2.4 | 2.5 | 2.6 | |
材积( | |||||
8 | 0.0130 | 0.0150 | 0.0160 | 0.0170 | 0.0180 |
10 | 0.0190 | 0.0220 | 0.0240 | 0.0250 | 0.0260 |
12 | 0.0270 | 0.0300 | 0.0330 | 0.0350 | 0.0370 |
14 | 0.0360 | 0.0400 | 0.0450 | 0.0470 | 0.0490 |
16 | 0.0470 | 0.0520 | 0.0580 | 0.0600 | 0.0630 |
18 | 0.0590 | 0.0650 | 0.0720 | 0.0760 | 0.0790 |
20 | 0.0720 | 0.0800 | 0.0880 | 0.0920 | 0.0970 |
22 | 0.0860 | 0.0960 | 0.1060 | 0.1110 | 0.1160 |
24 | 0.1020 | 0.1140 | 0.1250 | 0.1310 | 0.1370 |
若小李购买了两根紫檀原木,一根检尺长为![]() ,检尺径为
,检尺径为![]() ,另一根检尺长为
,另一根检尺长为![]() ,检尺径为
,检尺径为![]() ,根据上表,可知两根原木的材积之和为______
,根据上表,可知两根原木的材积之和为______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A. 甲地:总体均值为3,中位数为4 B. 乙地:总体均值为1,总体方差大于0
C. 丙地:中位数为2,众数为3 D. 丁地:总体均值为2,总体方差为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线E的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数).点P为曲线E上的动点,点Q为线段OP的中点.
(t为参数).点P为曲线E上的动点,点Q为线段OP的中点.
(1)求点Q的轨迹(曲线C)的直角坐标方程;
(2)若直线l交曲线C于A,B两点,点![]() 恰好为线段AB的三等分点,求直线l的普通方程.
恰好为线段AB的三等分点,求直线l的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDE中,DE∥AB,AC⊥BC,BC=2AC=2,AB=2DE,且D点在平面ABC内的正投影为AC的中点H且DH=1.

(1)证明:面BCE⊥面ABC
(2)求BD与面CDE夹角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com