练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】中国武汉于2019年10月18日至2019年10月27日成功举办了第七届世界军人运动会.来自109个国家的9300余名运动员同台竞技.经过激烈的角逐，奖牌榜的前3名如下：

    国家

    金牌

    银牌

    铜牌

    奖牌总数

    中国

    133

    64

    42

    239

    俄罗斯

    51

    53

    57

    161

    巴西

    21

    31

    36

    88

    某数学爱好者采用分层抽样的方式，从中国和巴西获得金牌选手中抽取了22名获奖代表.从这22名中随机抽取3人， 则这3人中中国选手恰好1人的概率为（ ）

    A.B.C.D.

    【答案】C

    【解析】

    先根据分层抽样确定中国选手的人数，再利用组合数根据古典概型的概率计算公式求解即可．

    解：中国和巴西获得金牌总数为154，按照分层抽样方法，

    22名获奖代表中有中国选手19个，巴西选手3个，

    故这3人中中国选手恰好1人的概率，

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】随着科技的发展，网购已经逐渐融入了人们的生活.在家里面不用出门就可以买到自己想要的东西，在网上付款即可，两三天就会送到自己的家门口，如果近的话当天买当天就能送到，或者第二天就能送到，所以网购是非常方便的购物方式.某公司组织统计了近五年来该公司网购的人数（单位：人）与时间（单位：年）的数据，列表如下：

    1

    2

    3

    4

    5

    24

    27

    41

    64

    79

    （1）依据表中给出的数据，是否可用线性回归模型拟合与的关系，请计算相关系数并加以说明（计算结果精确到0.01）.（若，则线性相关程度很高，可用线性回归模型拟合）

    附：相关系数公式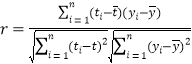 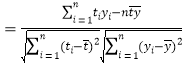，参考数据.

    （2）建立关于的回归方程，并预测第六年该公司的网购人数（计算结果精确到整数）.

    （参考公式： ，）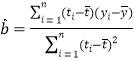

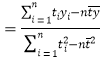    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中，为自然对数的底数.

    （1）当时，证明：对；

    （2）若函数在上存在极值，求实数的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学将100名高一新生分成水平相同的甲，乙两个“平行班”，每班50人.陈老师采用A,B两种不同的教学方式分别在甲，乙两个班级进行教改实验.为了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如下，计成绩不低于90分者为“成绩优秀”.

    （1）从乙班样本的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；

    （2）由以上统计数据填写下面2x2列联表，并判断是否有的把握认为“成绩优秀”与教学方式有关.


    甲班（A方式）

    乙班（B方式）

    总计

    成绩优秀




    成绩不优秀




    总计




    附：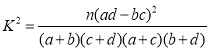

    /tr>

    P（

    0.25

    0.15

    0.10

    0.05

    0.025

    k

    1.323

    2.072

    2.706

    3.841

    5.024

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知方程只有一个实数根，则的取值范围是（ ）

    A.或B.或C.D.或

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy下，曲线C1的参数方程为（ 为参数），曲线C1在变换T：的作用下变成曲线C2．

    （1）求曲线C2的普通方程；

    （2）若m>1，求曲线C2与曲线C3：y=m|x|-m的公共点的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果无穷数列{an}的所有项恰好构成全体正整数的一个排列，则称数列{an}具有性质P．

    （Ⅰ）若an（k∈N*），判断数列{an}是否具有性质P，并说明理由，

    （Ⅱ）若数列{an}具有性质P，求证：{an}中一定存在三项ai，aj，ak（i＜j＜k）构成公差为奇数的等差数列；

    （Ⅲ）若数列{an}具有性质P，则{an}中是否一定存在四项ai，aj，ak，al，（i＜j＜k＜l）构成公差为奇数的等差数列？证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：经过点，右焦点到直线的距离为.

    （1）求椭圆的标准方程；

    （2）定义为，两点所在直线的斜率，若四边形为椭圆的内接四边形，且，相交于原点，且，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义：给定整数i，如果非空集合满足如下3个条件：

    ①；②；③，若，则.

    则称集合A为“减i集”

    （1）是否为“减0集”？是否为“减1集”？

    （2）证明：不存在“减2集”；

    （3）是否存在“减1集”？如果存在，求出所有“减1集”；如果不存在，说明理由.

    查看答案和解析>>

    同步练习册答案