（14分）集合
满足
=A，则称（）为集合A的一种分拆，并规定：当且仅当
时，（）与（
）为集合A的同一种分拆，则集合A={
}的不同分拆种数为多少？
阅读快车系列答案科目：高中数学 来源：2010年河南省高一年级月考数学试题 题型：解答题
（14分）集合
满足
=A，则称（）为集合A的一种分拆，并规定：当且仅当
时，（）与（
）为集合A的同一种分拆，则集合A={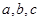
}的不同分拆种数为多少？
查看答案和解析>>
科目：高中数学 来源：0119 期末题 题型：填空题
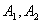满足
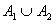=A，则称（
）为集合A的一种分拆，并规定：当且仅当
时，
）与（
）为集合A的同一种分拆，则集合A={a，b，c}的不同分拆种数为（ ）个。 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
＝
时，
=A,此时只有1种分拆；
或A，此时
}，B=
、
、
、
，此时
满足
=A，则称（
时，（
）为集合A的同一种分拆，则集合A={
}的不同分拆种数为多少？
满足
=A，则称（
时，（
）为集合A的同一种分拆，则集合A={
}的不同分拆种数为多少？