
(本题满分14分)甲、乙、丙3人投篮,投进的概率分别是![]() .
.
(Ⅰ)现3人各投篮1次,分别求3人都没有投进和3人中恰有2人投进的概率.
(Ⅱ)用ξ表示乙投篮4次的进球数,求随机变量ξ的概率分布及数学期望Eξ.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
(Ⅰ)记"甲投篮1次投进"为事件A1 , "乙投篮1次投进"为事件A2 , "丙投篮1次投进"为事件A3, "3人都没有投进"为事件A . 则 P(A1)=![]() , P(A2)= , P(A3)= ,
, P(A2)= , P(A3)= ,
∴ P(A) = P(![]() .
.![]() .
.![]() )=P(
)=P(![]() )·P(
)·P(![]() )·P(
)·P(![]() )
)
= [1-P(A1)] ·[1-P (A2)] ·[1-P (A3)]=(1-![]() )(1-)(1-)=
)(1-)(1-)=![]()
∴3人都没有投进的概率为![]() .设“3人中恰有2人投进"为事件B
.设“3人中恰有2人投进"为事件B
![]()
=(1-![]() )×
)×![]()
![]() +
+![]()
![]()
∴3人中恰有2人投进的概率为![]() ………………7分
………………7分
(Ⅱ)解法一: 随机变量ξ的可能值有0,1,2,3, 4, ξ~ B(4, ),
∴ P(ξ=k)=![]() ()k()
()k()![]() (k=0,1,2,3, 4) ,
(k=0,1,2,3, 4) ,
ξ的概率分布为
| ξ | 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
Eξ=np = 4× = ![]() . ………………14分
. ………………14分
解法二: 随机变量ξ的可能值有0,1,2,3, 4,
![]()
![]()
![]()
![]()
![]()
ξ的概率分布为:
| ξ | 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() +4×
+4×![]() =
= ![]() .………………14分
.………………14分


科目:高中数学 来源: 题型:
(本题满分14分)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为![]() .
.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
有时可用函数

描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(![]() ),
),![]() 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1) 证明:当![]() 时,掌握程度的增加量
时,掌握程度的增加量![]() 总是下降;
总是下降;
(2) 根据经验,学科甲、乙、丙对应的a的取值区间分别为![]() ,
,![]() ,
,
![]() .当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
.当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
查看答案和解析>>
科目:高中数学 来源:2011届江苏省南京六中高三下学期期中考试理数 题型:解答题
(本题满分14分)
甲打靶射击,有4发子弹,其中有一发是空弹.
(1)求空弹出现在第一枪的概率;
(2)求空弹出现在前三枪的概率;
(3)如果把空弹换成实弹,甲前三枪在靶上留下三个两两距离分别为3,4,5的弹孔 ,第四枪瞄准了三角形
,第四枪瞄准了三角形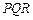 射击,第四个弹孔落在三角形
射击,第四个弹孔落在三角形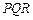 内
内 ,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三下学期期中考试理数 题型:解答题
(本题满分14分)
甲打靶射击,有4发子弹,其中有一发是空弹.
(1)求空弹出现在第一枪的概率;
(2)求空弹出现在前三枪的概率;
(3)如果把空弹换成实弹,甲前三枪在靶上留下三个两两距离分别为3,4,5的弹孔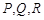 ,第四枪瞄准了三角形
,第四枪瞄准了三角形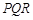 射击,第四个弹孔落在三角形
射击,第四个弹孔落在三角形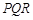 内,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
内,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com