【题目】如图，从参加环保知识竞赛的1200名学生中抽出
名，将其成绩（均为整数）整理后画出的频率分布直方图如下：观察图形，回答下列问题：
（1）
这一组的频数、频率分别是多少？
（2）估计这次环保知识竞赛的及格率。（分及以上为及格）
（3）若准备取成绩最好的300名发奖，则获奖的最低分数约为多少？
【答案】（1）频数15 频率0.25；（2）
；（2）82分
【解析】
（1）根据表中数据先计算出频率，然后再利用
乘以对应频率即可得到频数；
（2）根据图表计算出样本中的及格率，然后用样本估计总体即可得到这次环保知识竞赛的及格率；
（3）首先分析获奖的最低分数所在区间，然后利用所在区间中此最低分数前面的数据所占的比例乘以对应的区间长度，从而可求出最低分数的值.
（1）频率为：
，频数为：
；
（2）根据频率分布直方图可知，分及以上对应的频率为
，
用样本估计总体可知，估计这次环保知识竞赛的及格率为；
（3）因为
有：
人，
有
人，
所以最低分数所在区间为，且中获奖的有
人，所占区间总人数的比例为
，
所以最低分数为：
分.
科目：高中数学 来源： 题型：
【题目】某企业为确定下一年投入某种产品的研发费用，需了解年研发费用
（单位：千万元）对年销售量
（单位：千万件）的影响，统计了近10年投入的年研发费用
与年销售量
的数据，得到散点图如图所示：
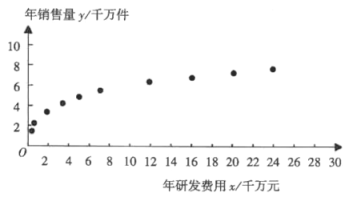
（1）利用散点图判断，
和
（其中
为大于0的常数）哪一个更适合作为年研发费用和年销售量的回归方程类型（只要给出判断即可，不必说明理由）.
（2）对数据作出如下处理：令
，
，得到相关统计量的值如下表：
根据（1）的判断结果及表中数据，求关于的回归方程；
（3）已知企业年利润
（单位：千万元）与
的关系为
（其中
），根据（2）的结果，要使得该企业下一年的年利润最大，预计下一年应投入多少研发费用？
附：对于一组数据
，
，
，
，其回归直线
的斜率和截距的最小二乘估计分别为
，
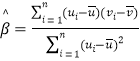查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下面几个命题中，假命题是（ ）
A. “若
，则
”的否命题
B. “
，函数
在定义域内单调递增”的否定
C. “
是函数
的一个周期”或“
是函数
的一个周期”
D. “
”是“
”的必要条件
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】关于曲线
，有如下结论：
①曲线
关于原点对称；
②曲线关于坐标轴对称；
③曲线是封闭图形；
④曲线不是封闭图形，且它与圆
无公共点；
⑤曲线与曲线
有
个交点，这点构成正方形.其中有正确结论的序号为__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，直线
与抛物线
（常数
）相交于不同的两点
、
，且
（
为定值），线段
的中点为
，与直线
平行的切线的切点为
（不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线，这个公共点为切点）．
（1）用
、
表示出点、点的坐标，并证明
垂直于
轴；
（2）求
的面积，证明的面积与、无关，只与有关；
（3）小张所在的兴趣小组完成上面两个小题后，小张连
、
，再作与、平行的切线，切点分别为
、
，小张马上写出了
、
的面积，由此小张求出了直线
与抛物线围成的面积，你认为小张能做到吗？请你说出理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于定义域为
的函数
，如果存在区间
，其中
，同时满足：
①
在
内是单调函数：②当定义域为时，的值域为，则称函数是区间上的“保值函数”，区间称为“保值函数”.
（1）求证：函数
不是定义域
上的“保值函数”；
（2）若函数
（
）是区间上的“保值函数”，求
的取值范围；
（3）对（2）中函数，若不等式
对
恒成立，求实数的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】过双曲线
的左焦点
作圆
的切线交双曲线的右支于点
，且切点为
，已知
为坐标原点，
为线段
的中点（点在切点的右侧），若
的周长为
，则双曲线的渐近线的方程为( )
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
