
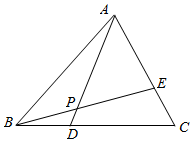
 在△ABC中,点D和E分别在边BC和AC上,且BC=3BD,CA=3CE,AD与BE交于点P,若$\overrightarrow{AP}$=m$\overrightarrow{AD}$,$\overrightarrow{BP}$=n$\overrightarrow{BE}$(m,n∈R),则m+n=$\frac{9}{7}$.
在△ABC中,点D和E分别在边BC和AC上,且BC=3BD,CA=3CE,AD与BE交于点P,若$\overrightarrow{AP}$=m$\overrightarrow{AD}$,$\overrightarrow{BP}$=n$\overrightarrow{BE}$(m,n∈R),则m+n=$\frac{9}{7}$. 分析 可根据条件用向量$\overrightarrow{AB},\overrightarrow{AE}$表示出向量$\overrightarrow{AP}$:$\overrightarrow{AP}=\frac{2m}{3}\overrightarrow{AB}+\frac{m}{2}\overrightarrow{AE}$,而三点B,P,E共线,这样便可得出$\frac{2m}{3}+\frac{m}{2}=1$,从而求出m的值,而同理可求出n的值,从而得出m+n的值.
解答 解:根据条件:$\overrightarrow{AP}=m\overrightarrow{AD}$
=$m(\overrightarrow{AB}+\overrightarrow{BD})$
=$m(\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC})$
=$m[\overrightarrow{AB}+\frac{1}{3}(\overrightarrow{AC}-\overrightarrow{AB})]$
=$m(\frac{2}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AE})$
∵B,P,E三点共线;
∴$\frac{2m}{3}+\frac{m}{2}=1$;
∴$m=\frac{6}{7}$;
同理求得n=$\frac{3}{7}$;
∴$m+n=\frac{9}{7}$.
故答案为:$\frac{9}{7}$.
点评 本题考查向量加法、减法和数乘的几何意义,以及向量数乘的运算,三点共线的充要条件:$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,且x+y=1.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | 9+3$\sqrt{5}$ | C. | 18 | D. | 12+3$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{1}{2}$] | C. | ($\frac{1}{2}$,1) | D. | [$\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 1 | C. | $\frac{5}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
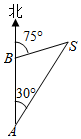 如图,一艘船下午13:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,14:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距9$\sqrt{2}$海里,则此船的航速为36海里/小时.
如图,一艘船下午13:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,14:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距9$\sqrt{2}$海里,则此船的航速为36海里/小时.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com