
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了50人,他们年龄大点频率分布及支持“生育二胎”人数如下表:
年龄 |
|
|
|
|
|
|
频率 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
(1)由以上统计数据填下面2乘2列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异:

(2)若对年龄在![]() 的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
【答案】(1)没有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;(2)![]() .
.
【解析】试题分析:(1)根据统计数据,可得![]() 列联表,根据列联表中的数据,计算
列联表,根据列联表中的数据,计算![]() 的值,即可得到结论;(2)利用列举法确定基本事件的个数,即可得出恰好两人都支持“生育二胎放开”的概率.
的值,即可得到结论;(2)利用列举法确定基本事件的个数,即可得出恰好两人都支持“生育二胎放开”的概率.
试题解析:(1)2乘2列联表:

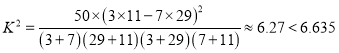 ,所以没有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异.
,所以没有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异.
(2)年龄在![]() 中支持“生育二胎”的4人分别为
中支持“生育二胎”的4人分别为![]() ,不支持“生育二胎”的人记为
,不支持“生育二胎”的人记为![]() ,
,
则从年龄在![]() 的被调查人中随机选取两人所有可能的结果有:
的被调查人中随机选取两人所有可能的结果有: ![]() ,
,
![]() .设“恰好这两人都支持“生育二胎””为事件
.设“恰好这两人都支持“生育二胎””为事件![]() ,则事件
,则事件![]() 所有可能的结果有:
所有可能的结果有: ![]() ,
, ![]() ,∴
,∴![]() ,所以对年龄在
,所以对年龄在![]() 的被调查人中随机选取两人进行调查时,恰好这两人都支持“生育二胎”的概率为
的被调查人中随机选取两人进行调查时,恰好这两人都支持“生育二胎”的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在R上的奇函数,且当x>0时,f(x)=1﹣x2 .
(1)求函数f(x)的解析式;
(2)作出函数f(x)的图象.
(3)若函数f(x)在区间[a,a+1]上单调,直接写出实数a的取值范围.(不必写出演算过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于0<a<1,给出下列四个不等式( )
①loga(1+a)<loga(1+ ![]() );
);
②loga(1+a)<loga(1+ ![]() );
);
③a1+a<a ![]() ;
;
④a1+a<a ![]() ;
;
其中成立的是( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高中学习过程中,同学们经常这样说:“数学物理不分家,如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论,现从该班随机抽取5名学生在一次考试中的数学和物理成绩,如下表:
编号 成绩 | 1 | 2 | 3 | 4 | 5 |
物理( | 90 | 85 | 74 | 68 | 63 |
数学( | 130 | 125 | 110 | 95 | 90 |
(1)求数学成绩![]() 对物理成绩
对物理成绩![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到
精确到![]() ),若某位学生的物理成绩为80分,预测他的数学成绩(结果精确到个位);
),若某位学生的物理成绩为80分,预测他的数学成绩(结果精确到个位);
(2)要从抽取的这五位学生中随机选出2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率.
(参考公式: 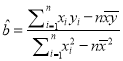 ,
, ![]() .)
.)
(参考数据: ![]() ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3x
(1)求函数f(x)的单调区间,并求函数f(x)的极值;
(2)若方程x3﹣3x﹣a+1=0有三个相异的实数根,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex+x﹣2,g(x)=lnx+x2﹣3,若实数a,b满足f(a)=0,g(b)=0,则( )
A.0<g(a)<f(b)
B.f(b)<g(a)<0
C.f(b)<0<g(a)
D.g(a)<0<f(b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com