
【题目】设l为曲线C:![]() 在点
在点![]() 处的切线.
处的切线.
(1)求l的方程;
(2)证明:除切点![]() 之外,曲线C在直线l的下方;
之外,曲线C在直线l的下方;
(3)求证:![]() (其中
(其中![]() ,
,![]() ).
).
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】
(1)求出切点处切线斜率,代入点斜式方程,可以求解;
(2)利用导数分析函数的单调性,进而分析出函数图象的形状,可得结论;
(3)法一,充分利用(2)的结果,对不等式左端进行放大,进一步放大为可以列项相消的形式来证明,法二,利用数学归纳法证明即可.
(1)设![]() (
(![]() ),则
),则![]() (
(![]() ),
),
从而曲线在点![]() 处的切线斜率为
处的切线斜率为![]() ,
,
于是切线方程为![]() ,即
,即![]() ,
,
因此直线l的方程为![]() .
.
(2)令![]() (
(![]() ),
),
则除切点![]() 之外,曲线C在直线l的下方等价于
之外,曲线C在直线l的下方等价于![]() (任意
(任意![]() ,
,![]() )恒成立.
)恒成立.
![]() 满足
满足![]() ,且
,且![]() (
(![]() ,
,![]() ),
),
当![]() 时,
时,![]() ,
,![]() ,从而
,从而![]() ,于是
,于是![]() 在
在![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() ,从而
,从而![]() ,于是
,于是![]() 在
在![]() 单调递增.
单调递增.
因此![]() (任意
(任意![]() ,
,![]() ),除切点
),除切点![]() 之外,曲线C在直线l的下方.
之外,曲线C在直线l的下方.
(3)方法1 由(2)可知![]() (任意
(任意![]() ,
,![]() ).
).
令![]() 得
得![]() ,即
,即![]() .
.
则![]() ,
,![]() ,…,
,…,![]() .
.
将以上各式相加得![]()
![]() ,
,
当![]() ,
,![]() 时,
时,![]() ,
,
![]() ,
,
![]()
![]() ,
,
所以当![]() ,
,![]() 时,
时,![]() ,结论成立.
,结论成立.
方法2:用数学归纳法证明:
①当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,左边
,左边![]() 右边,不等式成立.
右边,不等式成立.
②假设当![]() (
(![]() ,
,![]() )时,不等式成立,
)时,不等式成立,
即![]() ,
,
当![]() 时,
时,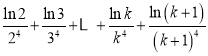
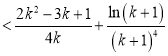 ,
,
只需证明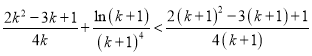 (*)
(*)
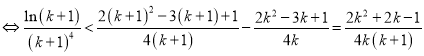
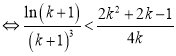 (**).
(**).
由(2)可知![]() (任意
(任意![]() ,
,![]() ),
),
则![]() (
(![]() ).
).
又当![]() ,
,![]() 时,
时,![]() ,
,
![]() ,
,
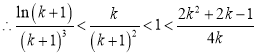 (
(![]() ).
).
所以(**)成立,从而(*)成立.
![]() 时,不等式成立.
时,不等式成立.
由①②可知,当![]() ,
,![]() 时,
时,![]() 成立.
成立.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若存在正数p,使得
,若存在正数p,使得![]() 对任意
对任意![]() 都成立,则称数列
都成立,则称数列![]() 为“拟等比数列”.
为“拟等比数列”.
![]() 已知
已知![]() ,
,![]() 且
且![]() ,若数列
,若数列![]() 和
和![]() 满足:
满足:![]() ,
,![]() 且
且![]() ,
,![]() .
.
![]() 若
若![]() ,求
,求![]() 的取值范围;
的取值范围;
![]() 求证:数列
求证:数列![]() 是“拟等比数列”;
是“拟等比数列”;
![]() 已知等差数列
已知等差数列![]() 的首项为
的首项为![]() ,公差为d,前n项和为
,公差为d,前n项和为![]() ,若
,若![]() ,
,![]() ,
,![]() ,且
,且![]() 是“拟等比数列”,求p的取值范围
是“拟等比数列”,求p的取值范围![]() 请用
请用![]() ,d表示
,d表示![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水果经销商为了对一批刚上市水果进行合理定价,将该水果按事先拟定的价格进行试销,得到一组销售数据,如表所示:
试销单价 | 16 | 17 | 18 | 19 | 20 |
日销售量 | 168 | 146 | 120 | 90 | 56 |
(1)已知变量![]() 具有线性相关关系,求该水果日销售量
具有线性相关关系,求该水果日销售量![]() (公斤)关于试销单价
(公斤)关于试销单价![]() (元/公斤)的线性回归方程,并据此分析销售单价
(元/公斤)的线性回归方程,并据此分析销售单价![]() 时,日销售量的变化情况;
时,日销售量的变化情况;
(2)若该水果进价为每公斤![]() 元,预计在今后的销售中,日销售量和售价仍然服从(1)中的线性相关关系,该水果经销商如果想获得最大的日销售利润,此水果的售价
元,预计在今后的销售中,日销售量和售价仍然服从(1)中的线性相关关系,该水果经销商如果想获得最大的日销售利润,此水果的售价![]()
![]() 应定为多少元?
应定为多少元?
(参考数据及公式:![]() ,
,![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,
,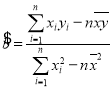 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新型冠状病毒疫情期间,商业活动受到很大影响某小型零售连锁店总部统计了本地区50家加盟店2月份的零售情况,统计数据如图所示.据估计,平均销售收入比去年同期下降40%,则去年2月份这50家加盟店的平均销售收入约为( )
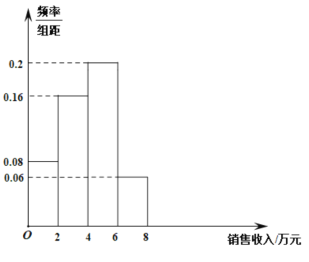
A.6.6万元B.3.96万元C.9.9万元D.7.92万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】11个兴趣班,若干学生参与(可重复参与),每个兴趣班人数相同(招满,人数未知).已知任意九个兴趣班包括了全体学生,而任意八个兴趣班没有包括全体学生求学生总人数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,则对于函数
为自然对数的底数,则对于函数![]() 有下列四个命题:
有下列四个命题:
命题1:存在实数![]() 使得函数
使得函数![]() 没有零点
没有零点
命题2:存在实数![]() 使得函数
使得函数![]() 有
有![]() 个零点
个零点
命题3:存在实数![]() 使得函数
使得函数![]() 有
有![]() 个零点
个零点
命题4:存在实数![]() 使得函数
使得函数![]() 有
有![]() 个零点
个零点
其中,正确的命题的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两类水果的质量(单位:![]() )分别服从正态分布
)分别服从正态分布![]() 、
、![]() ,其正态分布的密度曲线如图所示,则下列说法正确的是( )
,其正态分布的密度曲线如图所示,则下列说法正确的是( )
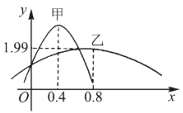
A.乙类水果的平均质量![]()
B.甲类水果的质量比乙类水果的质量更集中于平均值左右
C.甲类水果的平均质量比乙类水果的平均质量小![]()
D.乙类水果的质量服从的正态分布的参数![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com