
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(2)若![]() ,关于
,关于![]() 的方程
的方程![]() 有且仅有一个根, 求实数
有且仅有一个根, 求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,不等式
,不等式![]() 均成立, 求实数
均成立, 求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题(Ⅰ)求出函数的导数,得到函数的单调区间,从而求出函数的最大值即可;(Ⅱ)若a=-1,关于x的方程f(x)=kg(x)有且仅有一个根,即![]() ,有且只有一个根,令
,有且只有一个根,令![]() ,可得h(x)极大=h(2)=
,可得h(x)极大=h(2)=![]() ,h(x)极小=h(1)=
,h(x)极小=h(1)=![]() ,进而可得当k>
,进而可得当k>![]() 或0<k<
或0<k<![]() 时,k=h(x)有且只有一个根;(Ⅲ)设
时,k=h(x)有且只有一个根;(Ⅲ)设![]() ,因为
,因为![]() 在[0,2]单调递增,故原不等式等价于|f(x1)-f(x2)|<g(x2)-g(x1)在x1、x2∈[0,2],且x1<x2恒成立,当a≥-(ex+2x)恒成立时,a≥-1;当a≤ex-2x恒成立时,a≤2-2ln2,综合讨论结果,可得实数a的取值范围
在[0,2]单调递增,故原不等式等价于|f(x1)-f(x2)|<g(x2)-g(x1)在x1、x2∈[0,2],且x1<x2恒成立,当a≥-(ex+2x)恒成立时,a≥-1;当a≤ex-2x恒成立时,a≤2-2ln2,综合讨论结果,可得实数a的取值范围
试题解析:(1)当![]() 时,
时,![]() , 故
, 故![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增, 当
上单调递增, 当![]() 时,
时,![]() , 当
, 当![]() 时,
时,![]() , 故在区间
, 故在区间![]() 上
上![]() .
.
(2)当![]() 时, 关于
时, 关于![]() 的方程为
的方程为![]() 有且仅有一个实根, 则
有且仅有一个实根, 则![]() 有且仅有一个实根, 设
有且仅有一个实根, 设![]() ,则
,则![]() ,
,
因此![]() 在
在![]() 和
和![]() 上单调递减, 在
上单调递减, 在![]() 上单调递增,
上单调递增,![]() , 如图所示, 实数
, 如图所示, 实数![]() 的取值范围是
的取值范围是![]() .
.

(3)不妨设![]() ,则
,则![]() 恒成立.
恒成立.
因此![]() 恒成立, 即
恒成立, 即![]() 恒成立,
恒成立,
且![]() 恒成立, 因此
恒成立, 因此![]() 和
和![]() 均在
均在![]() 上单调递增,
上单调递增,
设![]() ,
,
则![]() 在上
在上![]() 上恒成立, 因此
上恒成立, 因此![]() 在
在![]() 上恒成立因此
上恒成立因此![]() ,而
,而![]() 在
在![]() 上单调递减, 因此
上单调递减, 因此![]() 时,
时,![]() .由
.由![]() 在
在![]() 上恒成立, 因此
上恒成立, 因此![]() 在
在![]() 上恒成立, 因此
上恒成立, 因此![]() ,设
,设![]() ,则
,则![]() .当
.当![]() 时,
时,![]() , 因此
, 因此![]() 在
在![]() 内单调递减, 在
内单调递减, 在![]() 内单调递增,因此
内单调递增,因此![]() .综上述,
.综上述,![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】下图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表.某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
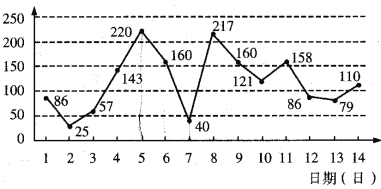
空气质量指数 | 污染程度 |
小于100 | 优良 |
大于100且小于150 | 轻度 |
大于150且小于200 | 中度 |
大于200且小于300 | 重度 |
(1)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(2)求此人到达当日空气质量优良的概率;
(3)求此人出差期间(两天)空气质量至少有一天为中度或重度污染的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程是![]() (t为参数),圆C的极坐标方程是ρ=4cos θ,求直线l被圆C截得的弦长.
(t为参数),圆C的极坐标方程是ρ=4cos θ,求直线l被圆C截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月25日-27日,北京召开第二届“一带一路”国际高峰论坛,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为 ( )
A. 198B. 268C. 306D. 378
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com