
分析 (1)利用相互独立事件的概率计算公式即可得出.
(2)利用相互独立事件与互斥事件的概率计算公式即可得出.
解答 解:(1)M与B1,B2,B3进行对抗赛获胜的事件分别为A,B,C,M至少获胜两场的事件为D,
则$P(A)=\frac{3}{4},P(B)=\frac{2}{3},P(C)=\frac{1}{2}$,由于事件A,B,C相互独立,
所以$P(D)=P(ABC)+P(AB\overline C)+P(A\overline BC)+P(\overline ABC)=\frac{3}{4}×\frac{2}{3}×\frac{1}{2}+\frac{3}{4}×\frac{2}{3}×\frac{1}{2}+\frac{3}{4}×\frac{1}{3}×\frac{1}{2}$$+\frac{1}{4}×\frac{2}{3}×\frac{1}{2}=\frac{17}{24}$,
由于$\frac{17}{24}$$>\frac{7}{10}$,所以M会入选最终的名单.
(2)M获胜场数X的可能取值为0,1,2,3,则$P(x=0)=\frac{1}{4}×\frac{1}{3}×\frac{1}{2}=\frac{1}{24}$,$P(x=1)=\frac{3}{4}×\frac{1}{3}×\frac{1}{2}+\frac{1}{4}×\frac{1}{3}×\frac{1}{2}+\frac{1}{4}×\frac{2}{3}×\frac{1}{2}=\frac{6}{24}$,
$P(x=2)=\frac{3}{4}×\frac{2}{3}×\frac{1}{2}+\frac{3}{4}×\frac{1}{3}×\frac{1}{2}+\frac{1}{4}×\frac{2}{3}×\frac{1}{2}=\frac{11}{24}$,$P(x=0)=\frac{3}{4}×\frac{2}{3}×\frac{1}{2}=\frac{6}{24}$.
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{24}$ | $\frac{6}{24}$ | $\frac{11}{24}$ | $\frac{6}{24}$ |
点评 本题考查了随机变量的概率分布列及其数学期望、相互独立与互斥事件的概率计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
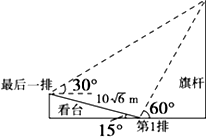 某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为$10\sqrt{6}$m(如图所示),则旗杆的高度为( )
某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为$10\sqrt{6}$m(如图所示),则旗杆的高度为( )| A. | 10m | B. | 30m | C. | 10m | D. | 10m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com