
 的分布列及数学期望。
的分布列及数学期望。 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
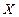 ,求随机变量
,求随机变量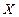 的分布列和均值.
的分布列和均值.| 9 | 2 | 8 | 8 |
| 8 | 5 | 5 | |
| 7 | 4 | 4 | 4 |
| 6 | 0 | 0 | |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
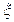
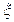 的概率分布;
的概率分布;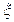 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,回答第三题正确的概率为
,回答第三题正确的概率为 ,且各题回答正确与否相互之间没有影响.记这位挑战者回答这三个问题的总得分为
,且各题回答正确与否相互之间没有影响.记这位挑战者回答这三个问题的总得分为 。
。 的概率分布和数学期望。
的概率分布和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
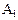 =“第i次抽到红球”,(
=“第i次抽到红球”,(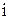 ="1," 2, 3)。试用
="1," 2, 3)。试用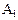 及
及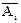 表示下列事件:
表示下列事件:查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com