
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是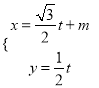 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,现提供
,现提供![]() 的大致图象的8个选项:
的大致图象的8个选项:
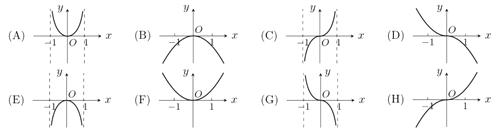
(1)请你作出选择,你选的是( );
(2)对于函数图像的判断,往往只需了解函数的基本性质.为了验证你的选择的正确性,请你解决
下列问题:
①![]() 的定义域是___________________;
的定义域是___________________;
②就奇偶性而言, ![]() 是______________________ ;
是______________________ ;
③当![]() 时,
时, ![]() 的符号为正还是负?并证明你的结论.
的符号为正还是负?并证明你的结论.
(解决了上述三个问题,你要调整你的选项,还来得及.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() 是椭圆的焦点,直线
是椭圆的焦点,直线![]() 的斜率为
的斜率为![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了纪念“中国红军长征90周年”,增强学生对“长征精神”的深刻理解,在全校组织了一次有关“长征”的知识竞赛,经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得20分,答错得0分.假设甲队中每人答对的概率均为![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为![]() ,
, ![]() ,
, ![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用![]() 表示乙队的总得分.
表示乙队的总得分.
(1)求![]() 的分布列和均值;
的分布列和均值;
(2)求甲、乙两队总得分之和等于40分且甲队获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有5名男志愿![]() 和3名女志愿者
和3名女志愿者![]() ,从中随机抽取4人接受甲种心理暗示,另4人接受乙种心理暗示.
,从中随机抽取4人接受甲种心理暗示,另4人接受乙种心理暗示.
(1)求接受甲种心理暗示的志愿者中包含![]() 但不包含
但不包含![]() 的频率.
的频率.
(2)用![]() 表示接受乙种心理暗示的女志愿者人数,求
表示接受乙种心理暗示的女志愿者人数,求![]() 的分布列与数学期望
的分布列与数学期望![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)若曲线![]() 在点
在点![]() 处的切线经过点
处的切线经过点![]() ,求
,求![]() 的值;
的值;
(2)若![]() 在区间
在区间![]() 上存在极值点,判断该极值点是极大值点还是极小值点,并求
上存在极值点,判断该极值点是极大值点还是极小值点,并求![]() 的取值范围;
的取值范围;
(3)若当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某物体一天中的温度![]() 是时间
是时间![]() 的函数,已知
的函数,已知![]() ,其中温度的单位是
,其中温度的单位是![]() ,时间的单位是小时,规定中午12:00相应的
,时间的单位是小时,规定中午12:00相应的![]() ,中午12:00以后相应的
,中午12:00以后相应的![]() 取正数,中午12:00以前相应的
取正数,中午12:00以前相应的![]() 取负数(例如早上8:00相应的
取负数(例如早上8:00相应的![]() ,下午16:00相应的
,下午16:00相应的![]() ),若测得该物体在中午12:00的温度为
),若测得该物体在中午12:00的温度为![]() ,在下午13:00的温度为
,在下午13:00的温度为![]() ,且已知该物体的温度在早上8:00与下午16:00有相同的变化率.
,且已知该物体的温度在早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度![]() 关于时间
关于时间![]() 的函数关系式;
的函数关系式;
(2)该物体在上午10:00至下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如下柱状图:

(1)从样本中任意选取2名学生,求恰好有一名学生的打分不低于4分的概率;
(2)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记![]() 表示两人打分之和,求
表示两人打分之和,求![]() 的分布列和
的分布列和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com